Предмет: Математика,
автор: ВиталийАлексеевич01
Дефферциальные уравнения Срочно 200б
Приложения:
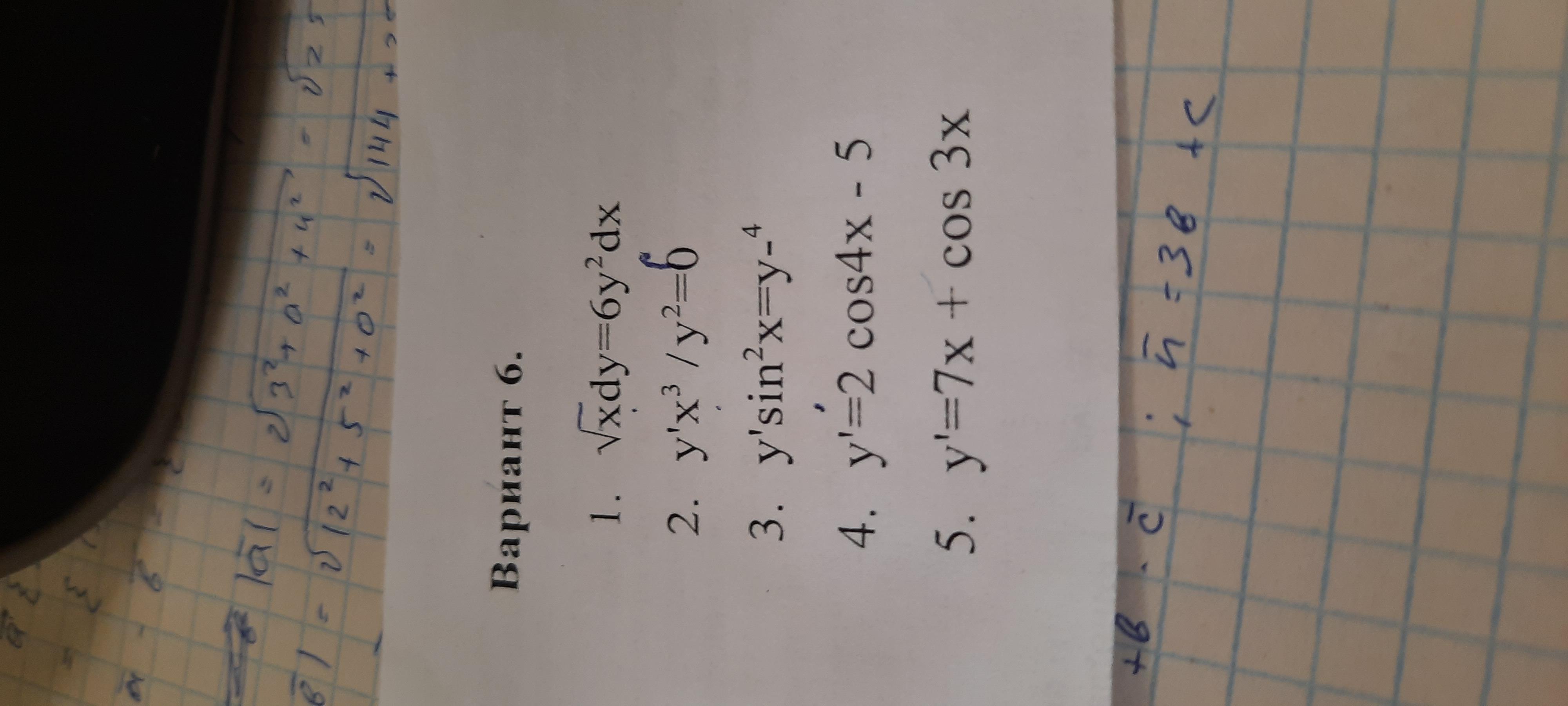
Ответы
Автор ответа:
0
1.
2.
3.
4.
5.
Похожие вопросы
Предмет: Окружающий мир,
автор: liliana20
Предмет: Русский язык,
автор: suhorukova82
Предмет: Русский язык,
автор: kcenui04
Предмет: История,
автор: Wimi