Предмет: Алгебра,
автор: EgorovaNatali
HELP PLEAS ALGEBRA ++++++++
Приложения:
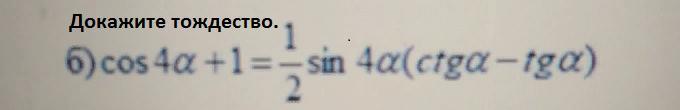
Ответы
Автор ответа:
1
Преобразуем правую и левую части равенства и если получим одинаковый результат, то значит тождество доказано .
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: немая1
Предмет: Русский язык,
автор: avyalla
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: НастюшаСтафеева