Предмет: Математика,
автор: Аноним
100 баллов!!!!
Найдите решение задачи Коши однородного линейного
дифференциального уравнения с постоянными коэффициентами
+ещё одна задачка
Найти общее решение дифференциального уравнения.
y два штриха - 13у (1 штрих)+12=x-1
Приложения:
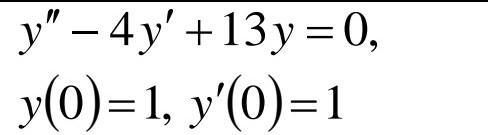
Ответы
Автор ответа:
1
Ответ:
1.
общее решение
частное решение
2.
это НЛДУ
1) Решаем ОЛДУ:
2) Подбираем у с неопределенными коэффициентми:
Подставляем в НЛДУ:
Общее решение:
Miroslava227:
да, забыла дописать
странно, должен быть
тогда ду выглядит так у"-13у'=х-13?
о логике переносим 12 в правую сторону
по*
я к тому, что у 12 должен быть у, иначе странно задавать уравнение таким образом
Похожие вопросы
Предмет: Английский язык,
автор: wwwjulia1979
Предмет: Қазақ тiлi,
автор: apleskan
Предмет: Другие предметы,
автор: 2015XaKeR2015
Предмет: Математика,
автор: АкцентФыр
Предмет: Алгебра,
автор: apchivillia