Question

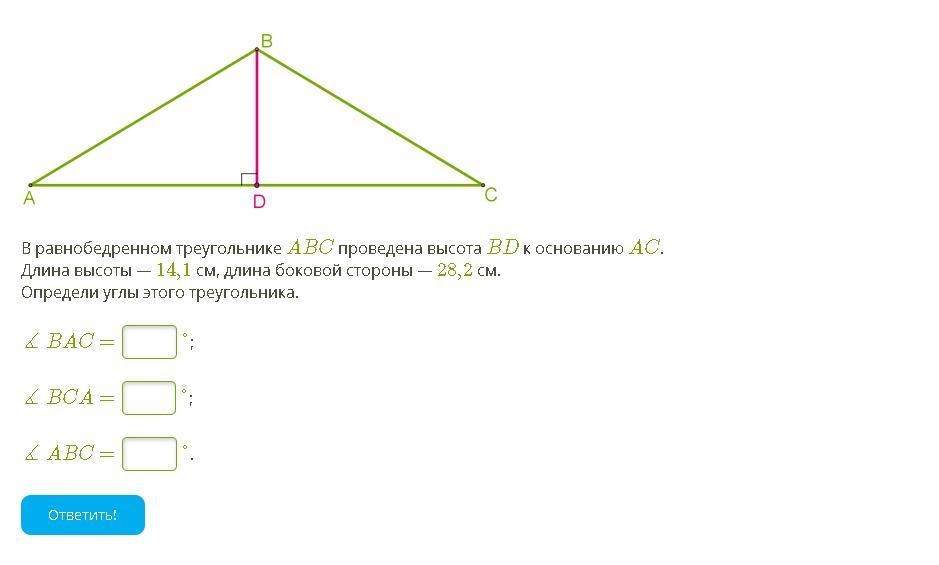
В равнобедренном треугольнике ABC проведена высота BD к основанию AC.
Длина высоты — 14,1 см, длина боковой стороны — 28,2 см.
Определи углы этого треугольника.

∡ BAC =
°;

∡ BCA =
°;

∡ ABC =
°.

Answer 1

Ответ:

∡ BAC = 30°; ∡ BCA = 30°; ∡ ABC = 120°.

Объяснение:

1) В прямоугольном треугольнике ABD боковая сторона АВ = 28,2 см является гипотенузой, а высота BD = 14,1 см - катетом.

Так как данный катет в 2 раза меньше гипотенузы, то это означает, что угол ВАС, против которого лежит катет ВD, равен 30°.

∡ BAC = 30°

2) В равнобедренном треугольнике углы при основании равны, поэтому:

∡ BCA = ∡ BAC = 30°

3) Угол АВС равен разности между суммой внутренних углов треугольника (180°) и углами при основании:

∡ ABC = 180 -  ∡ BCA -  ∡ BAC  = 180 - 30 - 30 = 120°.

Ответ: ∡ BAC = 30°; ∡ BCA = 30°; ∡ ABC = 120°.