Question

Пожалуйста завтра задавать!!!!

Ди­зай­нер, чтобы до­пол­нить пре­крас­ный ри­су­нок в виде рав­но­бед­рен­но­го тре­уголь­ни­ка на стене за­каз­чи­ка, решил про­ве­сти пря­мую. Автор ри­сун­ка, яв­ля­ясь боль­шим лю­би­те­лем гео­мет­рии, решил про­ве­сти её сле­ду­ю­щим об­ра­зом: она пройдёт через вер­ши­ну угла при ос­но­ва­нии и раз­де­лит ис­ход­ный тре­уголь­ник на два тре­уголь­ни­ка, каж­дый из ко­то­рых также яв­ля­ет­ся рав­но­бед­рен­ным. По­мо­ги­те ди­зай­не­ру найти углы ис­ход­но­го рав­но­бед­рен­но­го тре­уголь­ни­ка.​

Answer 1

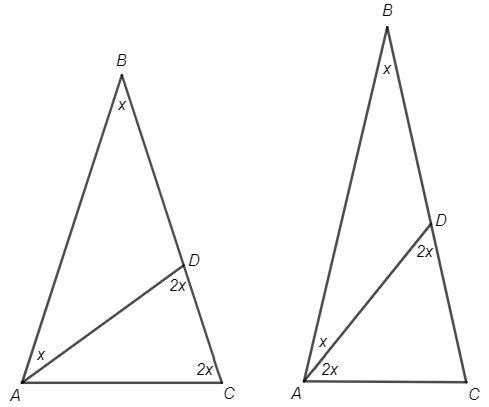
AC - основание равнобедренного △ABC.

Провели прямую AD.

В равнобедренном △ABD:

AD не является основанием, так как AB и BD не равны.

Предположим, что BD является основанием. Тогда ∠ADB - острый, смежный ∠ADC - тупой. В равнобедренном △ADC тупой угол может быть только против основания, но ∠DAC и ∠С не равны. Следовательно BD не является основанием.

Установили, что AB - основание равнобедренного △ABD.

Пусть ∠B=∠BAD =x

Тогда ∠ADC=2x (внешний угол)

В равнобедренном △ADC:

AC не является основанием, так как ∠DAC и ∠С не равны.

Возможны два случая:

1) DC является основанием

∠ADC=∠C=∠A =2x

∠A+∠B+∠C=180° => 5x=180° => x=36°

∠B =36°

∠A=∠C =72°

2) AD является основанием

∠ADC=∠DAC=2x => ∠A=∠C=3x

∠A+∠B+∠C=180° => 7x=180° => x=180°/7

∠B =180°/7  ~25,71°

∠A=∠C =540°/7  ~77,14°