Предмет: Математика,
автор: bayjigitisakba
Помогите, дам" много" баллов
Приложения:
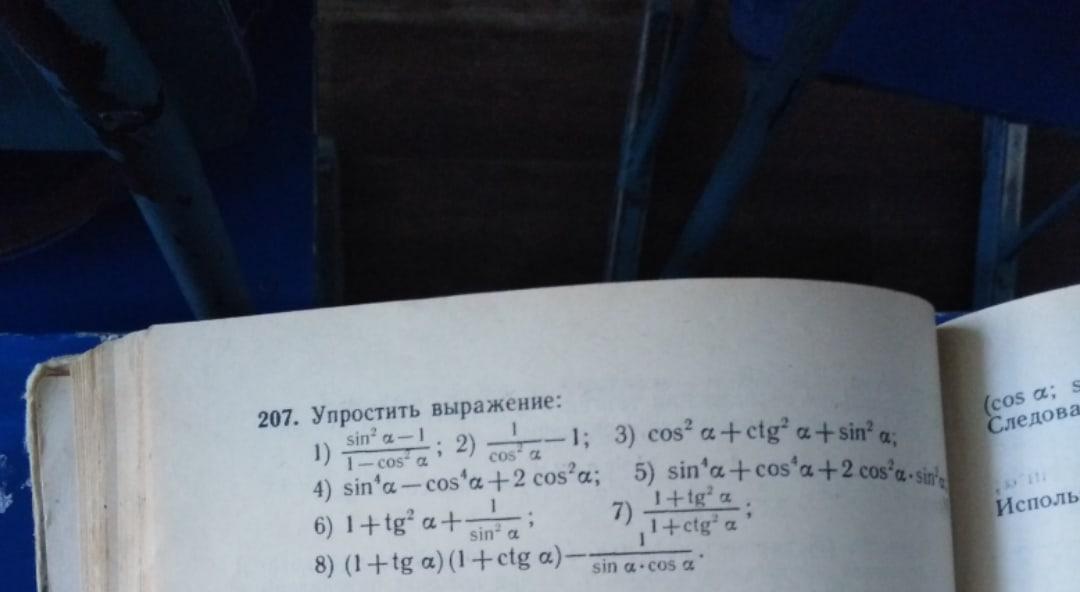
Ответы
Автор ответа:
0
Ответ:
1)
2)
3)
4)
5)
6)
7)
8)
Похожие вопросы
Предмет: Русский язык,
автор: Maks1005
Предмет: Українська мова,
автор: Вiра
Предмет: Русский язык,
автор: diegorova1994
Предмет: Другие предметы,
автор: danilkolan9294
Предмет: География,
автор: Аноним