Предмет: Алгебра,
автор: erkeandakulov
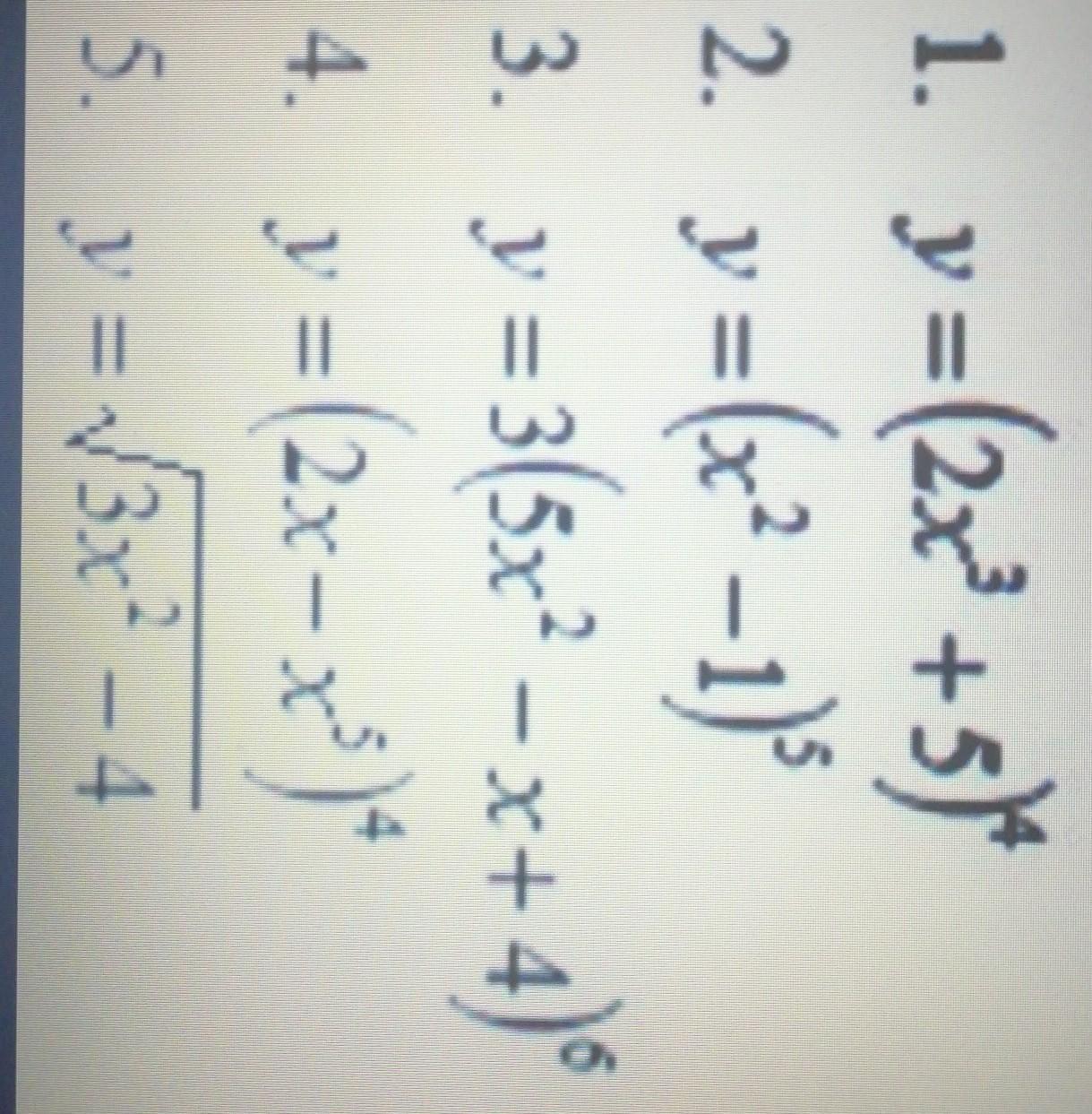
Найти пройзводную..........
Приложения:
Ответы
Автор ответа:
1
1.
2.
3.
4.
5.
Автор ответа:
1
Ответ:
1.
2.
3.
4.
5.
Объяснение:
Производная сложной функции h(x) находится по формуле:
Смотрите фотографии!
Приложения:


Похожие вопросы
Предмет: Українська мова,
автор: алькаупс
Предмет: Немецкий язык,
автор: Vitka11111
Предмет: Английский язык,
автор: eyats
Предмет: Физика,
автор: anhelova02
Предмет: Химия,
автор: 1v2a3r4v5a6r7a