Предмет: Алгебра,
автор: Jusperrr
Довести тотожність
sin( π\4 + 2) = cos (π\4 -2)
Приложения:
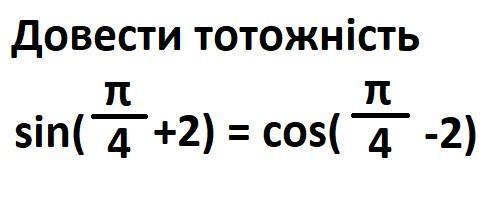
Ответы
Автор ответа:
1
Ответ:
yulyaivanchenko65:
Добрый день,не могли бы вы помочь мне если вам не трудно конечно, https://znanija.com/task/43657526,я буду безумно вам благодарна за ваше милосердие ко мне,с меня 5 звёзд и лучший ответ, зарание спасибо за помош!!!!!!!!!!!!!!!!!!!!1
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: ксюша387
Предмет: Немецкий язык,
автор: okolotvina
Предмет: Українська мова,
автор: Аноним
Предмет: Русский язык,
автор: corsa1337