Помогите с заданием
Длины сторон треугольника АВС соответственно равны: ВС = 15 см, АВ = 13 см, АС = 4 см. Через сторону АС проведена плоскость α, составляющая с плоскостью данного треугольника угол 300. Найдите расстояние от вершиныВ до плоскости α.
И начертите схему к заданию пж треугольник что тут короче написано
Ответы
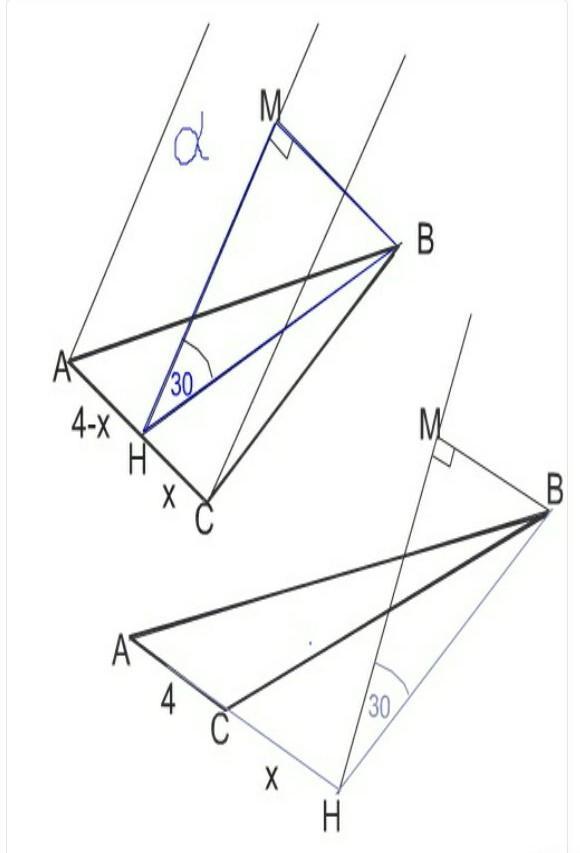
Проведем высоту ВН= h треугольника АВС.
Расстояние от С до Н обозначим х, от Н до А 4-х
Высоту вычислим из треугольника ВНС и ВНА
h²=ВС²-х²=13²-х²
h²=ВА²=АН²= 15²-(4-х)²
h²=15²-(4-х)²
13²-х²=15²-(4-х)²
169-х²=225-16+8х-х²
169 - х²=225 - 16 + 8х - х²
8х= - 40
х= -5 см
----------------------
(Отрицательное значение х указыает на то, что основание высоты h треугольника АВС находится на продолжнении его основания, и, следовательно, угол АСВ - тупой.
Можно было бы, зная, что треугольник тупоугольный, расстояние АН обозначить как 4+х. Результат был бы тот же.)
-------------------------
h²=169-25=144
h=12
Рассмотрим треугольник ВМН. (Второй рисунок дала для большей наглядности. При решении можно использовать дополнительное построение, в котором В1М1=ВМ, а угол В1АМ1 равен 30 градусов)
Расстояние ВМ от вершины В до плоскости α - катет прямоугольного треугольника ВМН, противолежащий углу 30 градусов, и потому равен половине высоты ВН треугольника АВС
ВМ=12:2=6 см