Предмет: Математика,
автор: ramazan70972
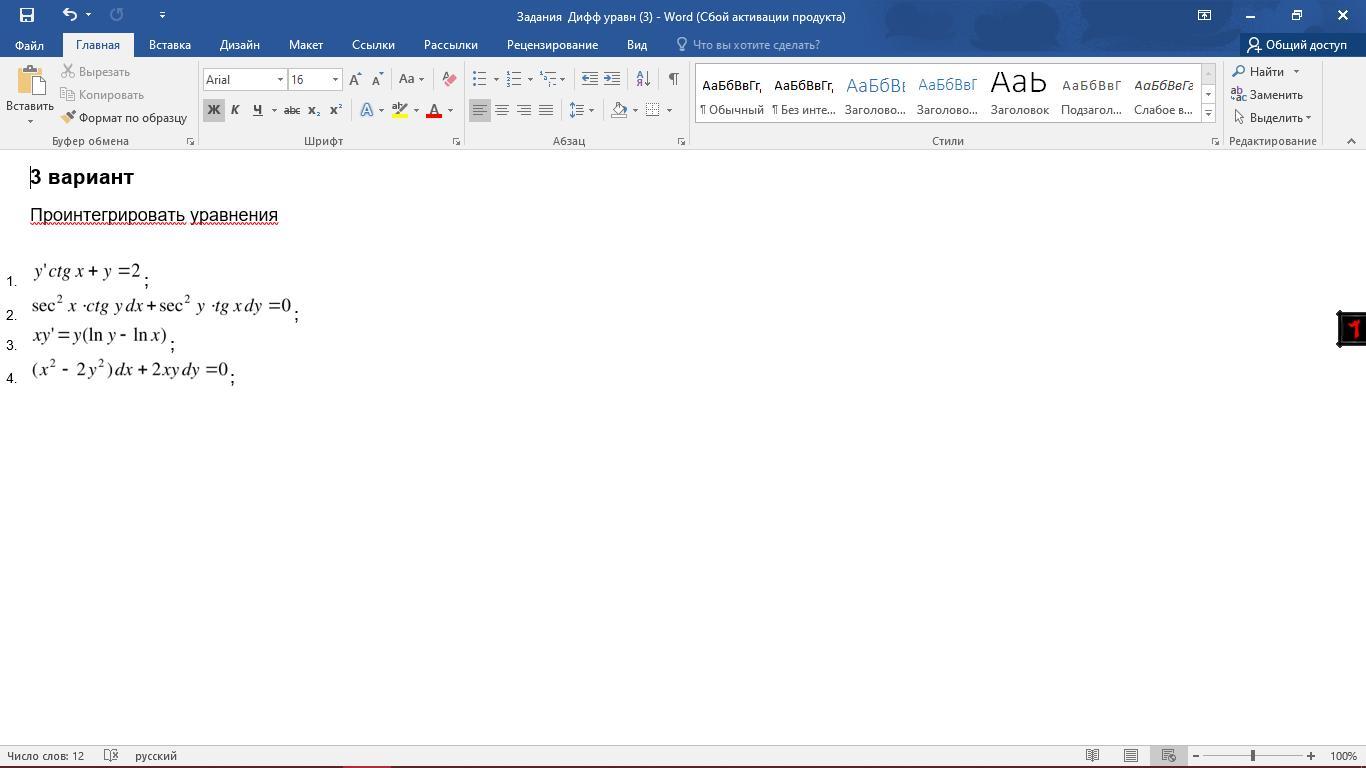
Помогите пожалуйста проинтегрировать уравнения
Приложения:
Ответы
Автор ответа:
1
Ответ:
1.
общее решение
2.
общее решение
3.
общее решение
4.
общее решение
nxnfejdbi:
здравствуйте
можете помочь
Похожие вопросы
Предмет: Українська література,
автор: innakyruljak
Предмет: Беларуская мова,
автор: kisaaaaaaaa2
Предмет: Українська мова,
автор: JRV
Предмет: Русский язык,
автор: Валерыч2005
Предмет: Математика,
автор: Komlyk