Предмет: Математика,
автор: КатяRita
Тригонометрия. Помогите решить, пожалуйста
Приложения:
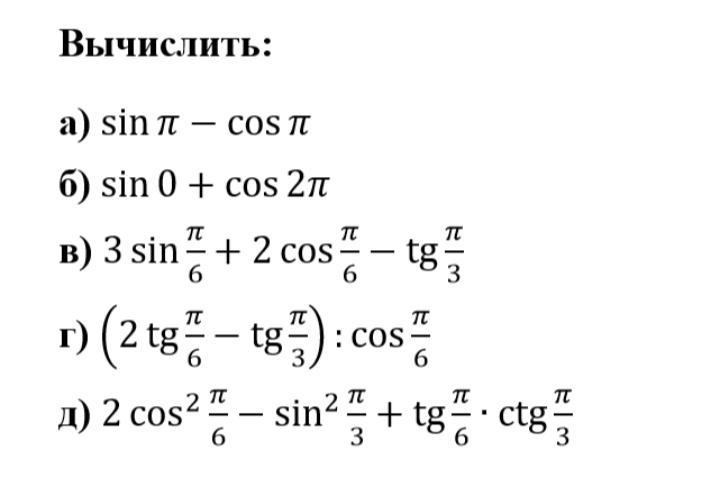
Ответы
Автор ответа:
1
1. 0-(-1)=1
2. 0+1=1
3.
4.
5.
NNNLLL54:
sin^2П/3=3/4 , а не 3/2 ... исправьте
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: kristinaca1988
Предмет: Русский язык,
автор: ninuly2004
Предмет: Английский язык,
автор: zhenuylka
Предмет: Алгебра,
автор: KARIN1230
Предмет: Другие предметы,
автор: Vitalikeky