Предмет: Геометрия,
автор: Kata2921
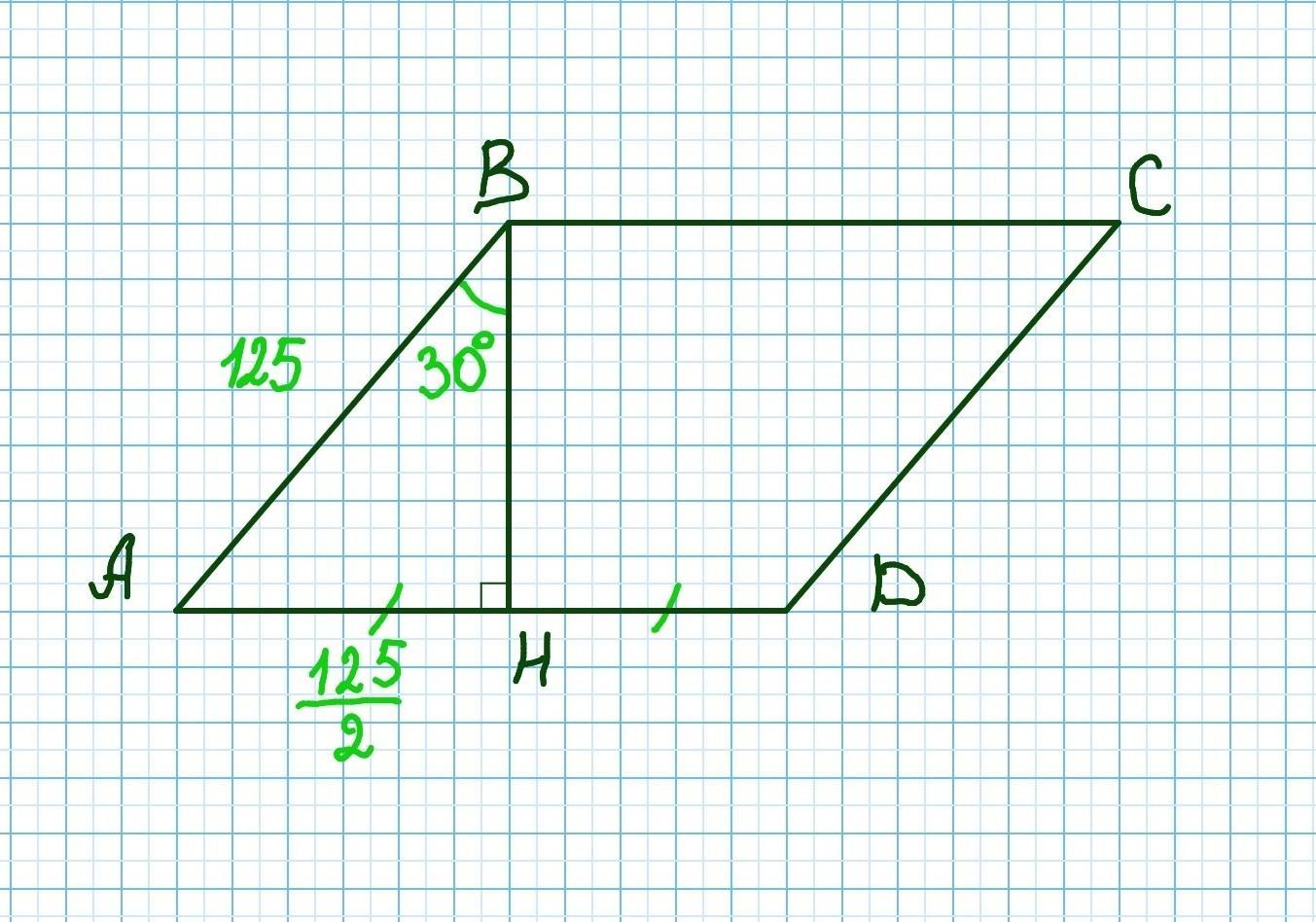
Одна из сторон ромба равна 125, а его высота, проведённая из вершины
угла, делит сторону, к которой она проведена, пополам. Найди высоту ромба.
Ответы
Автор ответа:
0
Ответ:
62,5√3 ед
Объяснение:
Ромб - это параллелограмм у которого все стороны равны.
Из вершины В проведена высота ВН, которая делит сторону AD пополам. BH⟂AD. AH=HD.
Рассмотрим прямоугольный △ABH(∠H=90°).
AB=125ед, AH=½AD=½•AB (т.к. AB=AD, как стороны ромба).
Следовательно катет AH равен половине гипотенузы, значит он лежит напротив угла в 30°.
- Если катет прямоугольного треугольника равен половине гипотенузы то угол лежащий против этого катета равен 30°.
ВН=АВ•cos30°=125•(√3/2)=62,5√3 ед
Высота ромба равна 62,5√3 ед
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: АннаЛюсия
Предмет: Русский язык,
автор: айдай5
Предмет: Українська мова,
автор: oljaslnshk
Предмет: Математика,
автор: BabelGum
Предмет: Литература,
автор: nastya19876