Предмет: Математика,
автор: lemurity
Нужно подробное решение с ответом
Приложения:
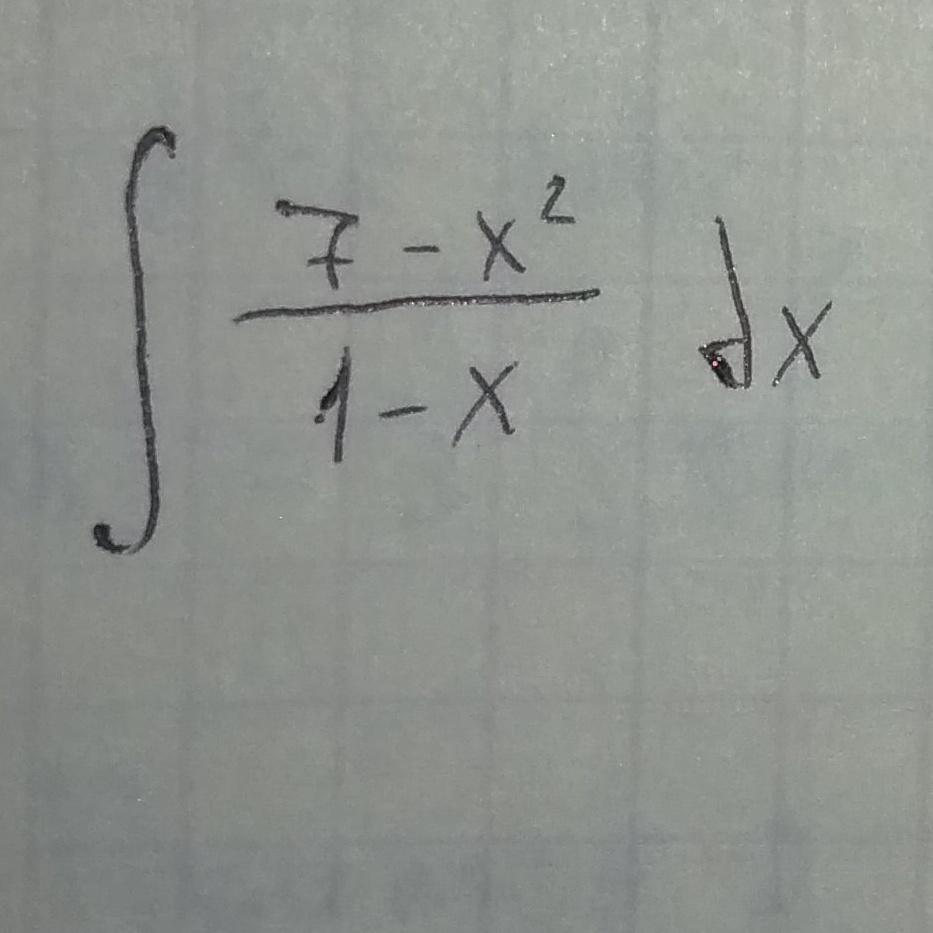
Ответы
Автор ответа:
0
Ответ:
Автор ответа:
1
Ответ:
Решение смотри на фотографии
Приложения:
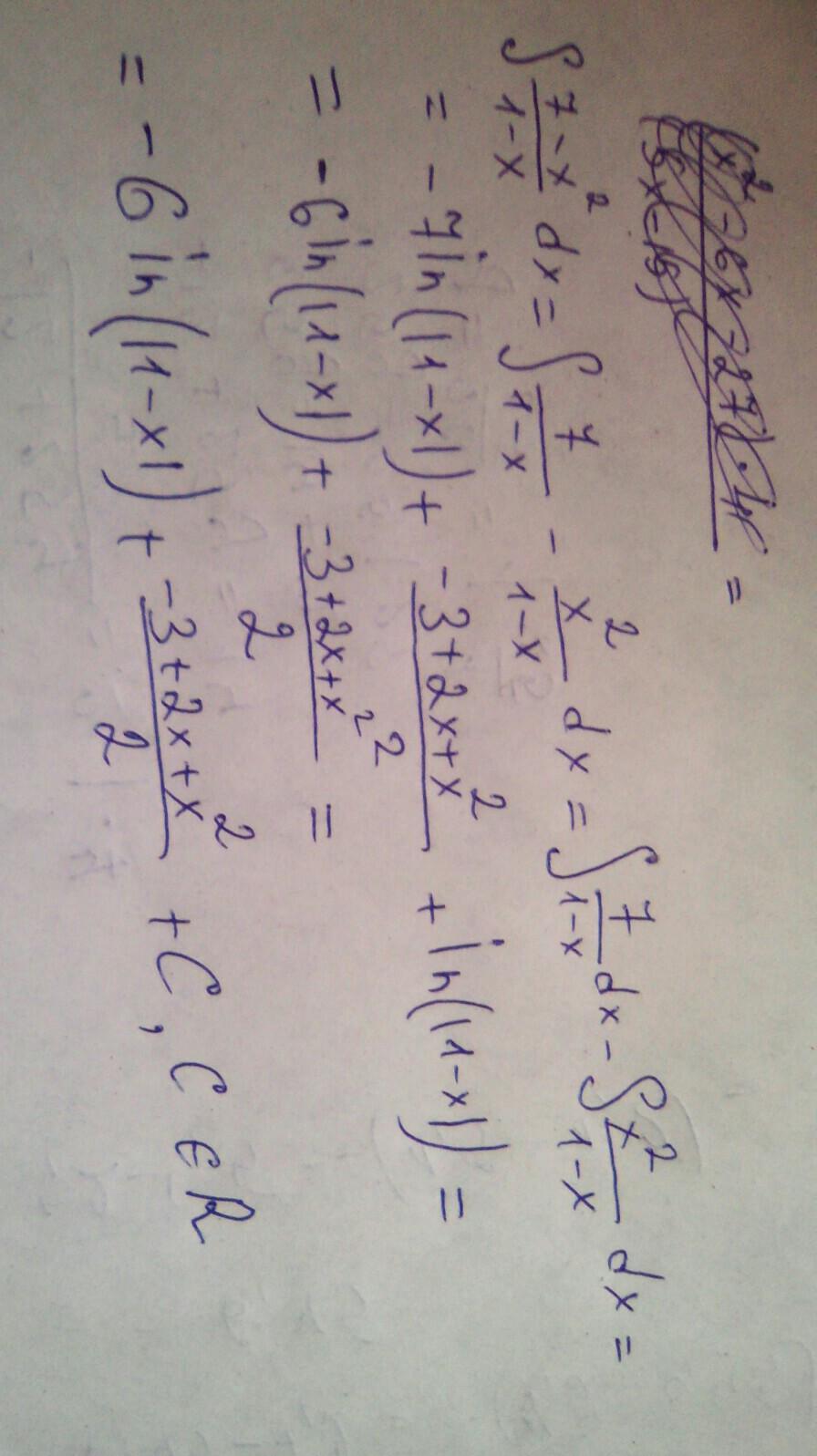
Похожие вопросы
Предмет: Русский язык,
автор: максюши
Предмет: Русский язык,
автор: DanyaPlz
Предмет: Русский язык,
автор: anya123456789000
Предмет: Алгебра,
автор: artemkhulup