Предмет: Математика,
автор: kirahardman
Помогите найти производную!
Приложения:
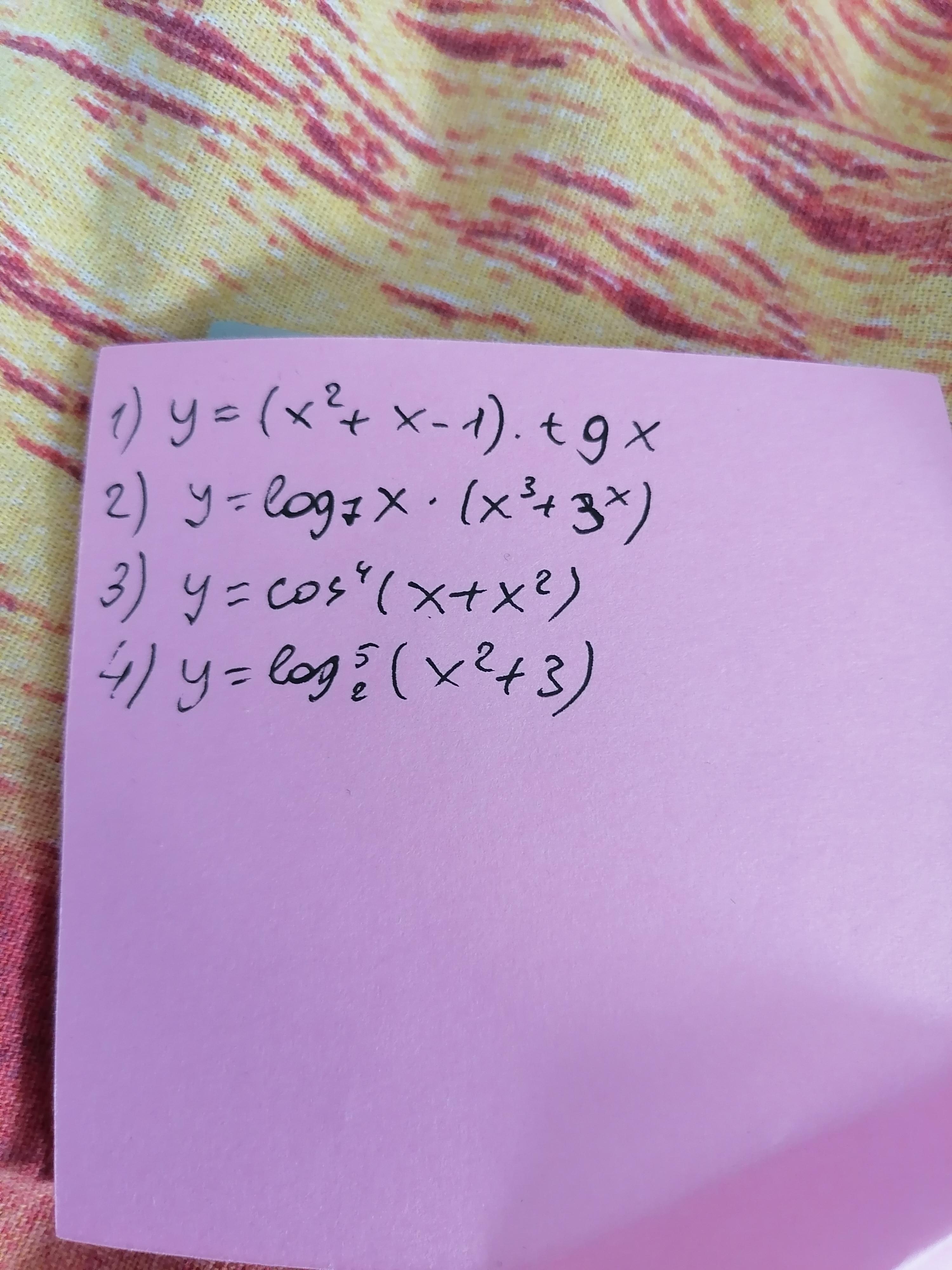
Ответы
Автор ответа:
1
Ответ:
1
2
3
4
DoctorEmmettBrown:
Здравствуйте, можно вас спросить, как я понял, что вы здесь один из самых умных 1) как ты этого добился? 2) как я могу развиваться на этом сайте?
Похожие вопросы
Предмет: Қазақ тiлi,
автор: мухтар3
Предмет: Русский язык,
автор: TheMrStive
Предмет: Русский язык,
автор: 093119977
Предмет: Математика,
автор: statsitskiy1122
Предмет: Русский язык,
автор: fara84kzp5n1m5