Предмет: Математика,
автор: yaronoprienko208
За темою Диференціальні рівняння.
Приложения:
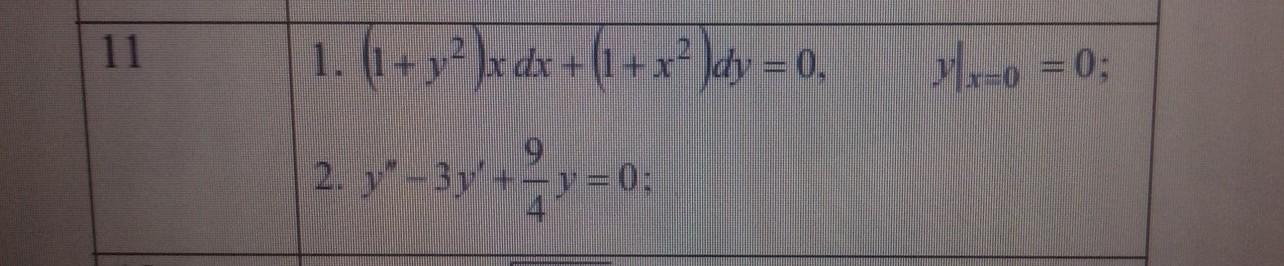
Ответы
Автор ответа:
1
Ответ:
1.
Это ДУ с разделяющимися переменными
общее решение
частное решение
2. Это линейное однородное ДУ
общее решение
yaronoprienko208:
Спасибо большое тебе!
Похожие вопросы
Предмет: Другие предметы,
автор: Сауле11111
Предмет: Английский язык,
автор: Marino4ka2222
Предмет: Русский язык,
автор: Kardashian
Предмет: Геометрия,
автор: Al1a888
Предмет: Алгебра,
автор: ATOM34