Предмет: Алгебра,
автор: tamararynd
Решыте пожалуйста 1d)f) и #2;3 даю 50 балов срочно нужно с решением не просто ответ
Приложения:

Ответы
Автор ответа:
1
Ответ:
1.
d)
n принадлежит Z.
f)
n принадлежит Z.
2.
квадратное уравнение имеет корни, когда дискриминант больше или равен 0.
Ответ: а - любое число.
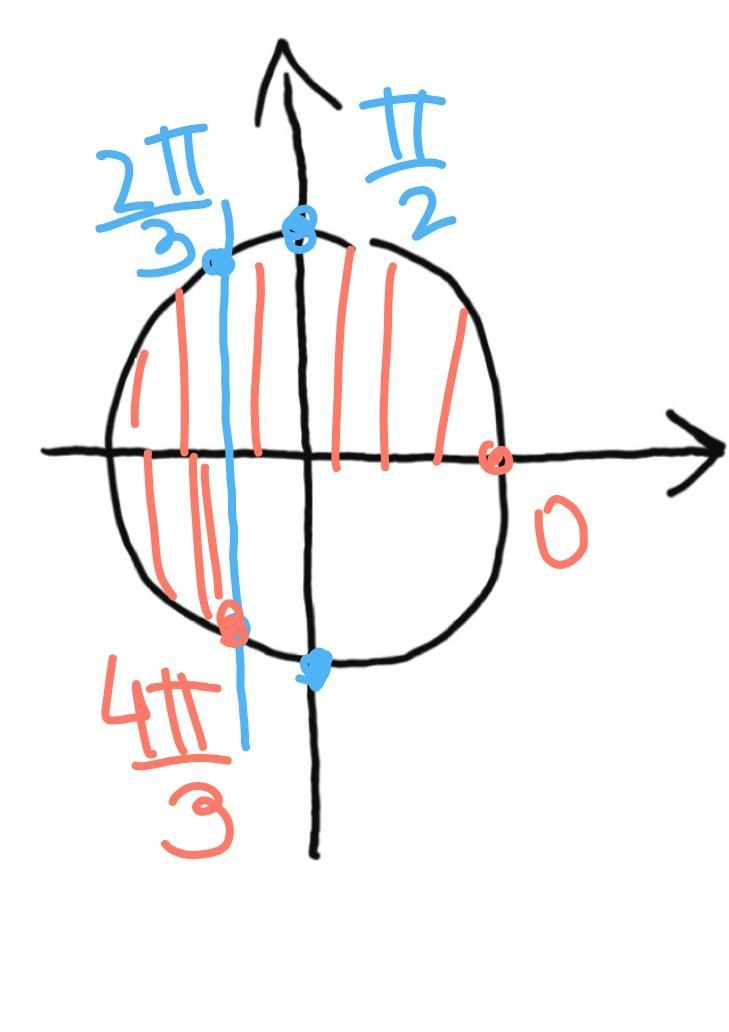
3.
Отметим корни на окружности:
рисунок
при а = 4П/3
Приложения:
tamararynd:
Огромное спасибо❤️
Ля как много
Похожие вопросы
Предмет: Русский язык,
автор: makarandmarika
Предмет: Українська мова,
автор: МашаХартій
Предмет: Українська мова,
автор: KatePanda2015
Предмет: Геометрия,
автор: nikshapar