Предмет: Математика,
автор: nastac917
Обчислити невизначений інтеграл заміною змінних. Треба дуже детальний розв'язок. (Вища математика) ТЕРМІНОВО!
Приложения:
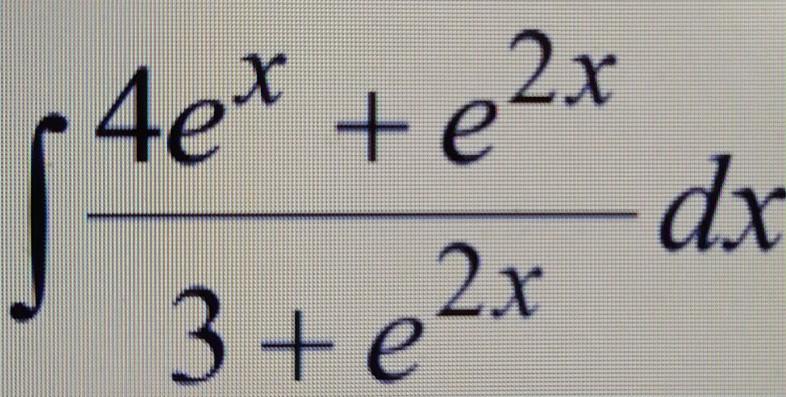
Ответы
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: madina9992
Предмет: Русский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: 34567891011121
Предмет: Английский язык,
автор: yauto4ka
Предмет: Геометрия,
автор: ThePaper