Question

Равнобедренный треугольник со сторонами AB = BC = 4см, сторона AC принадлежит плоскости "a". Треугольник ABC с плоскостью "a" образует угол 45 градусов, а сторона AB к плоскости "a" наклонена под 30 градусов.
Посчитайте площадь треугольника ABC.

Answer 1

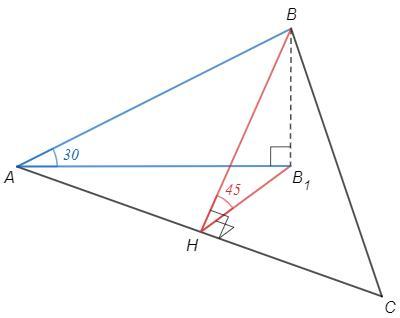
Опустим перпендикуляр BB1 на плоскость a

Угол между наклонной и плоскостью - угол между наклонной и ее проекцией, ∠BAB1 =30

Опустим перпендикуляр BH на AC

BB1⊥a, BH⊥AC => B1H⊥AC (т о трех перпендикулярах)

Угол между плоскостями - угол между перпендикулярами к общей прямой, ∠BHB1 =45

BB1/AB =sin30

BB1/BH =sin45

cos(ABH) =BH/AB =sin30/sin45 =1/2 : 1/√2 =1/√2 => ∠ABH=45

BH - высота и биссектриса (△ABC - р/б), ∠ABC =2∠ABH =90

S(ABC) =1/2 AB*BC =4*4/2 =8 (см^2)