Предмет: Математика,
автор: jonchannel
Тригнометрия. Помогите решить, пожалуйста
Приложения:
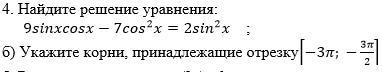
Ответы
Автор ответа:
1
Ответ:
n принадлежит Z.
на промежутке:
Приложения:
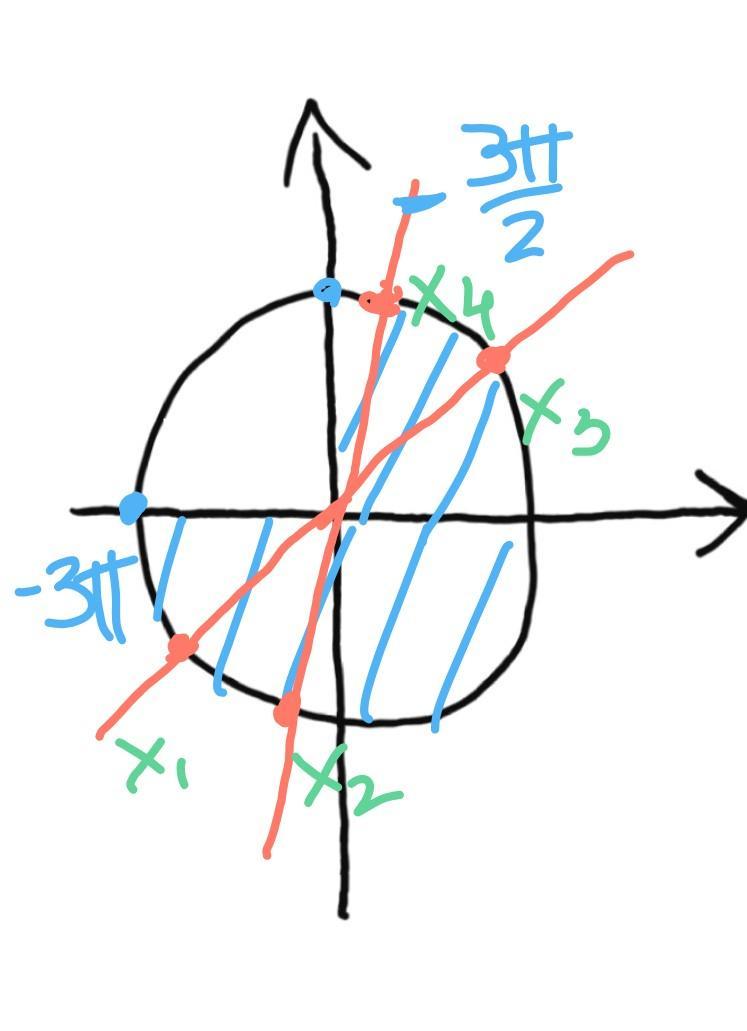
буду признателен <3
Похожие вопросы
Предмет: Українська мова,
автор: derazhenko86
Предмет: Русский язык,
автор: msgula1970
Предмет: Русский язык,
автор: аня646
Предмет: Математика,
автор: fralova7
Предмет: Другие предметы,
автор: Аноним
https://znanija.com/task/43648268