Предмет: Алгебра,
автор: nikapisareva36
Помогите решить задание
Приложения:
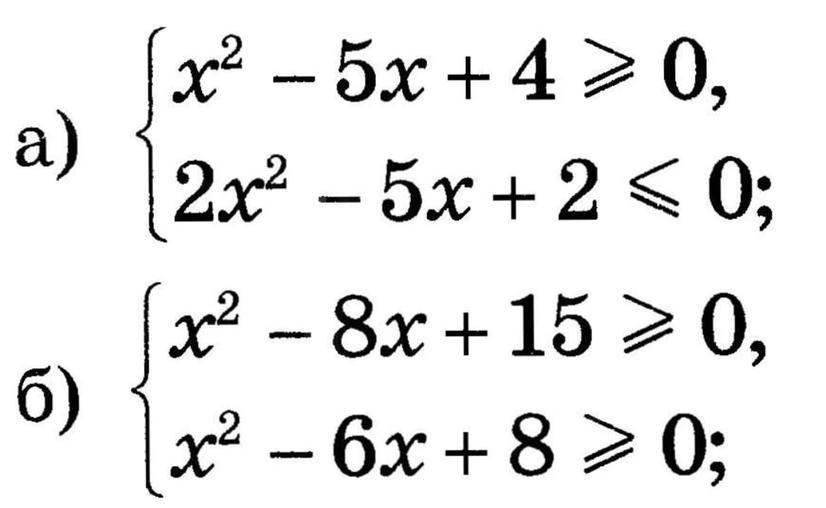
Ответы
Автор ответа:
1
Відповідь:
a)
1)х∈(-∞;1]∪[4;+∞)
2)x∈[1/2;2]
находим пересечение :
х∈[1/2;1]
Пояснення:
Похожие вопросы
Предмет: Русский язык,
автор: tbeanov
Предмет: Английский язык,
автор: диёра24
Предмет: Русский язык,
автор: pavlovayapavl
Предмет: Окружающий мир,
автор: ajdar666
Предмет: Математика,
автор: 5192