Question

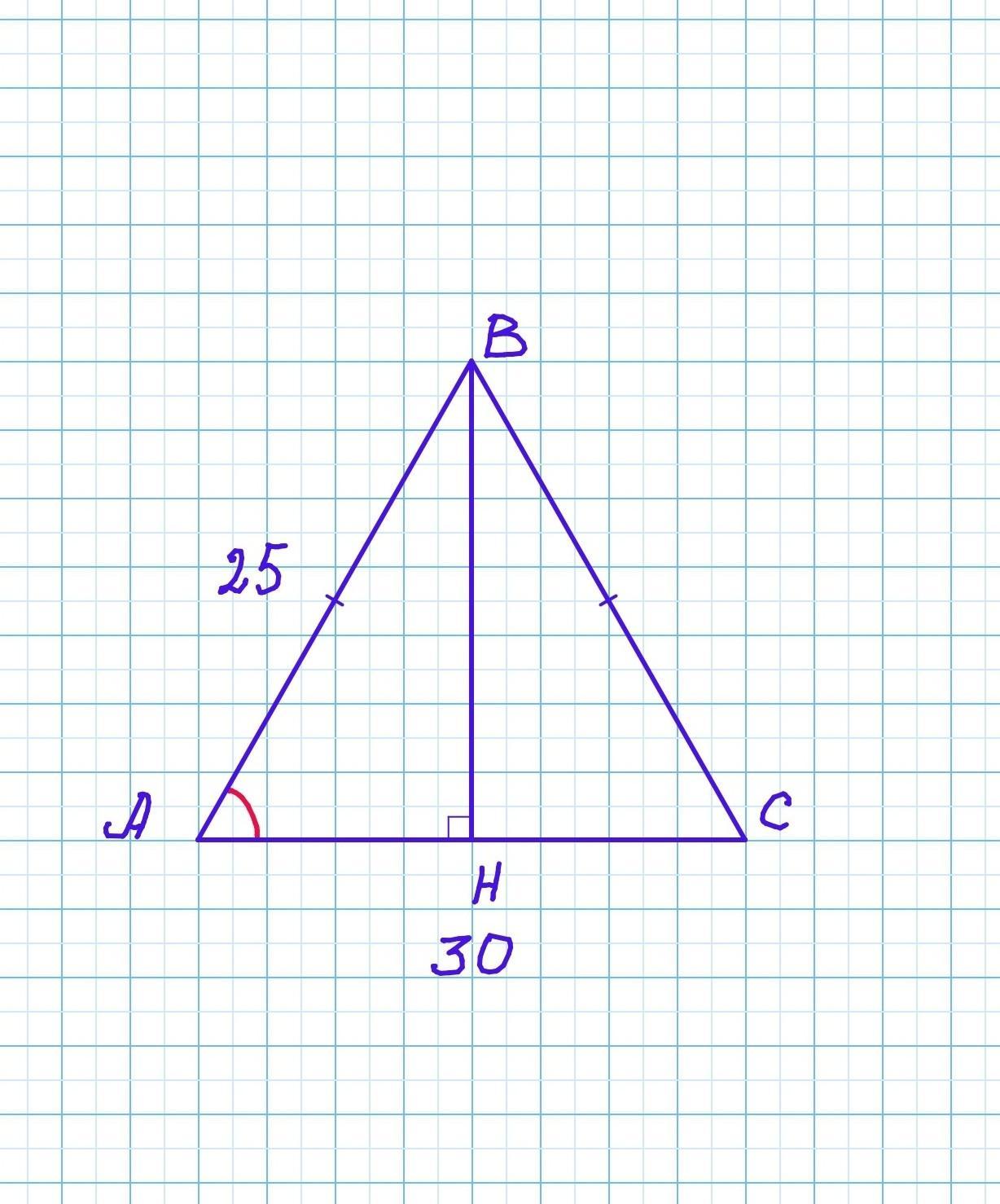
В треугольнике ABC стороны AB и BC равны. Найдите sinA, если AB=25, AC=30.
СРОЧНО ПОЖАЛУЙСТА!!!!!

Answer 1

В треугольнике ABC стороны AB и BC равны. Найдите sinA, если AB=25, AC=30.

Ответ:

sin∠A=0,8

Объяснение:

Проведём высоту ВН. ВН⟂АС. Так как △АВС - равнобедренный, то ВН является также медианой.

АН=НС=½•АС=½•30=15 ед

Рассмотрим прямоугольный треугольник АВН.

Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.

$cos\angle A= \dfrac{AH}{AB} = \dfrac{15}{25} = \dfrac{3}{5}$

Из основного тригонометрического тождества:

cos²A+sin²A=1,

найдём sin∠A.

$sin\angle A= \sqrt{1 - cos^{2}\angle A} = \sqrt{1 - ( { \frac{3}{5} })^{2} } = \\ \\ = \sqrt{1 - \frac{9}{25} } = \sqrt{ \frac{25 - 9}{25} } = \sqrt{ \frac{16}{25} } = \frac{4}{5} = 0,8$