Помогите пожалуйста
Решите уравнения:
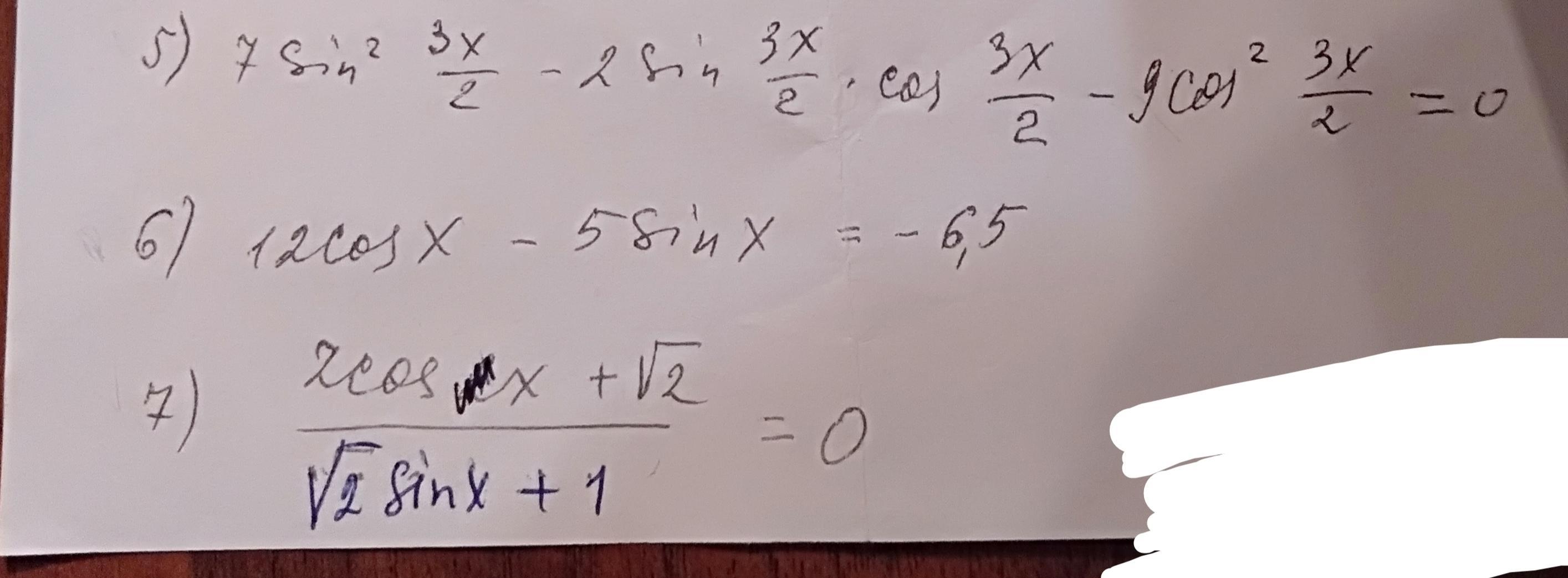
Ответы
5) 7sin^2(3x/2) - 2sin(3x/2)*cos(3x/2) - 9cos^2(3x/2) = 0
Делим всё на cos^2(3x/2)
7tg^2(3x/2) - 2tg(3x/2) - 9 = 0
Делаем замену tg(3x/2) = y
7y^2 - 2y - 9 = 0
(y+1)(7y-9) = 0
y1 = tg(3x/2) = -1
3x/2 = -Π/4 + Πk
x1 = -Π/6 + 2Π/3*k, k € Z
y2 = tg(3x/2) = 9/7
3x/2 = arctg(9/7) + Πk
x2 = 2/3*arctg(9/7) + 2Π/3*k, k € Z
Ответ: x1 = -Π/6 + 2Π/3*k;
x2 = 2/3*arctg(9/7) + 2Π/3*k, k € Z
6) 12cos x - 5sin x = -6,5
Переходим к половинному аргументу.
12cos^2(x/2) - 12sin^2(x/2) - 10sin(x/2)*cos(x/2) = -6,5cos^2(x/2) - 6,5sin^2(x/2)
18,5cos^2(x/2) - 5,5sin^2(x/2) - 10sin(x/2)*cos(x/2) = 0
Получили такое же уравнение, как 5). Умножаем на -2 и делим на cos^2(x/2).
11tg^2(x/2) + 20tg(x/2) - 37 = 0
Замена tg(x/2) = y
11y^2 + 20y - 37 = 0
D/4 = 10^2 - 11(-37) = 100 + 407 = 507
y1 = tg(x/2) = (10-√507)/11
x1 = 2arctg ((10-√507)/11) + 2Πk, k € Z
y2 = tg(x/2) = (10+√507)/11
x2 = 2arctg ((10+√507)/11) + 2Πk, k € Z
Ответ: x1 = 2arctg((10-√507)/11) + 2Πk;
x2 = 2arctg((10+√507)/11) + 2Πk, k € Z
7) (2cos x + √2) / (√2*sin x + 1) = 0
Если дробь равна 0, то числитель равен 0, а знаменатель нет.
{ 2cos x + √2 = 0
{ √2*sin x + 1 ≠ 0
Решаем:
{ cos x = -√2/2
{ sin x ≠ -1/√2
Получаем:
{ x1 = 3Π/4 + 2Πk; x2 = 5Π/4 + 2Πk, k € Z
{ x1 ≠ 5Π/4 + 2Πk; x2 ≠ 7Π/4 + 2Πk, k € Z
Корень 5Π/4 + 2Πk - лишний.
Ответ: x = 3Π/4 + 2Πk, k € Z