Предмет: Математика,
автор: kalintseva03
Исследуйте на монотонность функцию
f(x)=(9sinx-9cosx-19)e^x
Приложения:
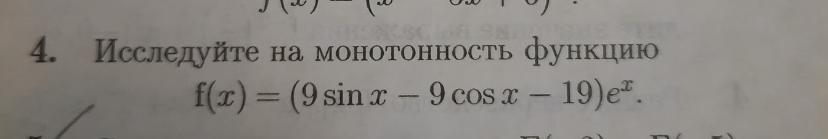
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
f(x)=(9sinx-9cosx-19)eˣ
найдем критические точки и интервалы смены знака
f'(x) = (9sinx-9cosx-19)'*eˣ + (9sinx-9cosx-19)*(eˣ)' = (9cosx +9sinx)eˣ +(9sinx-9cosx-19)eˣ=
=eˣ(9cosx +9sinx +9sinx-9cosx-19) = (18sinx-19)eˣ
(18sinx-19)eˣ=0
это уравнение не имеет решений, т.е критических точек нет
при этом
f'(x) тождественно не равна 0
и f'(x) < 0
значит функция f(x) строго убывающая на всей области существования
Похожие вопросы
Предмет: Русский язык,
автор: KiraKlar1990
Предмет: Окружающий мир,
автор: Вероника20022008
Предмет: Английский язык,
автор: Nasiaa
Предмет: Математика,
автор: annaverzilina47