Предмет: Алгебра,
автор: axmax2004xxx
Решите пожалуйста логарифмическое неравенство.
Приложения:
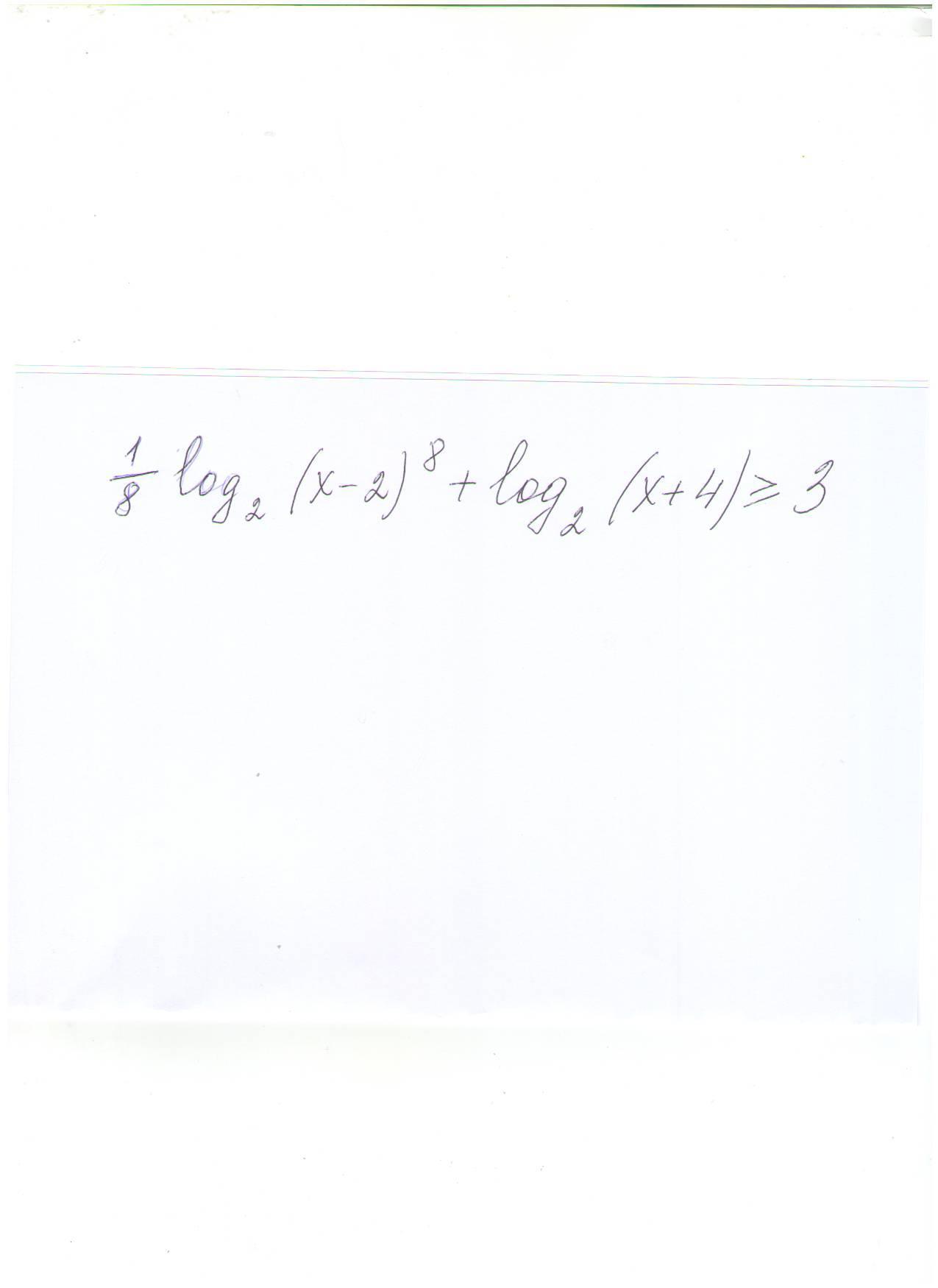
Ответы
Автор ответа:
1
Объяснение:
ОДЗ: (х-2)⁸>0 x≠2 x+4>0 x>-4 ⇒ x∈(-4;2)U(2;+∞).
-∞__+__-1-√17__-__-1+√17__+__+∞
Ответ: x∈[-1+√17;+∞).
axmax2004xxx:
Благодарен
Удачи.
Помогите пожалуйста с любой задачей в моем профиле
Похожие вопросы
Предмет: Українська мова,
автор: ukraine2316
Предмет: Английский язык,
автор: Tigran2016
Предмет: Окружающий мир,
автор: urakovaarina20
Предмет: Литература,
автор: Katy8547
Предмет: Музыка,
автор: 00Софа00