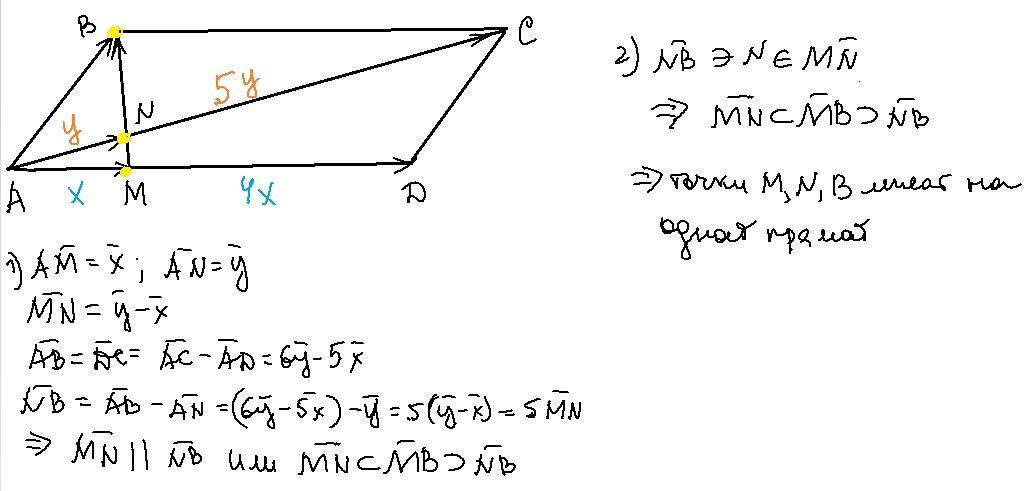
Задача на картинке. Никаких координат нет, нужно как-то по-другому решить... Пришлёте ответ - будет вам вечная память.
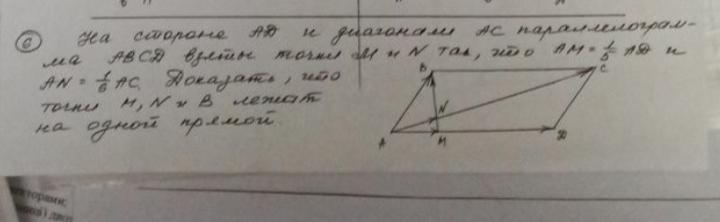
Ответы
Вижу стрелки. Подразумевается решение через векторы (оно в другом ответе), но можно и так:
1) Пусть AM = a, AN = b. Тогда по условию NC = 5b, а MD = 4a, BC = 5a. Пусть угол NAM = α. Т.к AC - диагональ, то и угол BCA = углу NAM = α, ведь диагональ пересекает два параллельных основания. Треугольники AMN и BCN подобны по углу и образующим его сторонам (Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны).
2) Пусть угол BNC = β, тогда из подобия ANM тоже = β. Два накрест лежащих угла равны только в том случае, если они образованы не более чем двумя прямыми. Поэтому трёх прямых, как на картинке, быть не может. Если A, N и C лежат на одной прямой, значит и B, N, M лежат на одной прямой, чтд
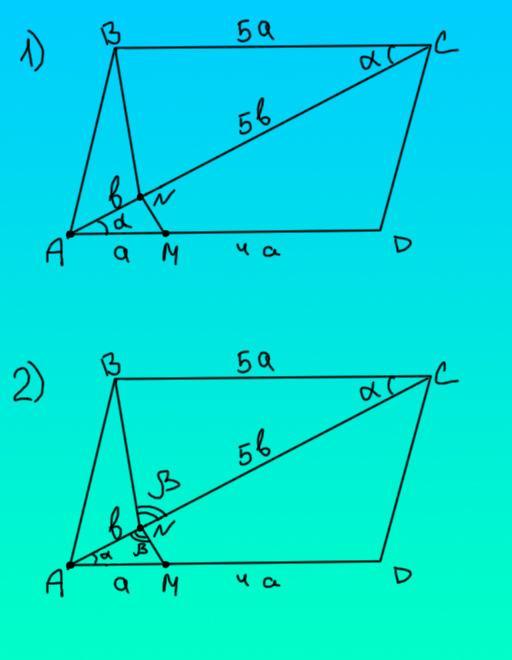
Ответ:
см. решение в прикрепленном фото
Объяснение: