Предмет: Математика,
автор: segop43648
13 задание, ЕГЭ профиль
Приложения:
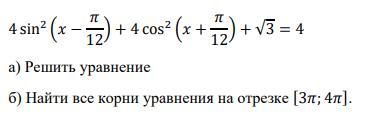
Ответы
Автор ответа:
2
Ответ:
(см. объяснение)
Пошаговое объяснение:
Найдем корни уравнения, принадлежащие промежутку .
Задание выполнено!
segop43648:
огромное спасибо :)
Похожие вопросы
Предмет: Українська мова,
автор: apodgaetskiy
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: OlesyaSubbota
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: Baiganaevadilya