Question

вычислить предварительно сделав рисунок площадь фигуры ограниченной линиями
y=x^2 ;y=x^3

Answer 1

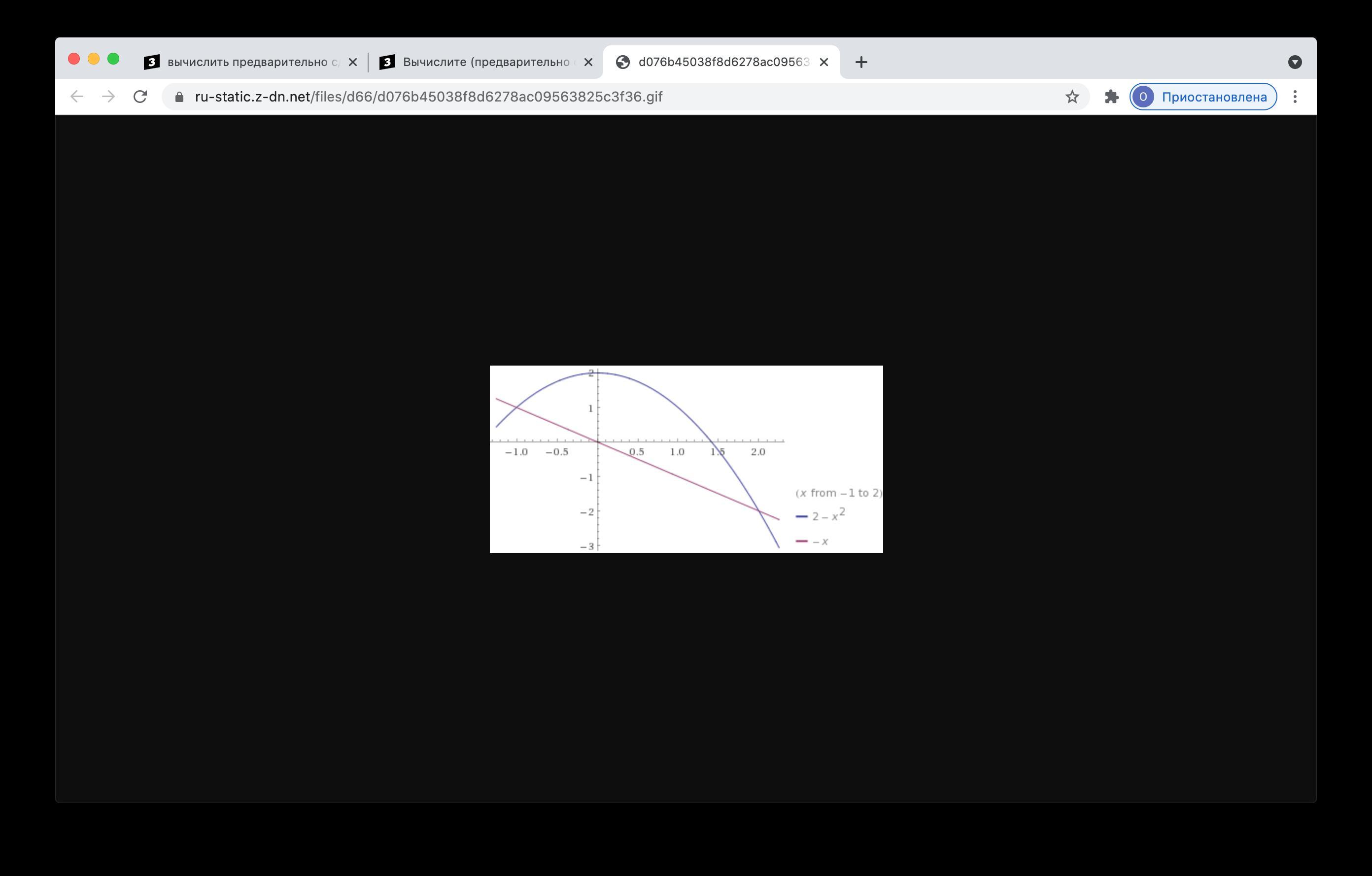
графически определяем точки пересечения графиков (-1; 1) ; (2; -2)

(можно аналитически - решить систему)

интервал интегрирования [-1; 2]

площадь фигуры

S =  ¯¹∫² -x2+2 - (-x) = -x^3/3 +2x +x^2/2 ¯¹∫² =

= -(2)^3/3 +2*2 +2^2/2  - (-(-1)^3/3 +2*(-1) +(-1)^2/2)  =4.5

ОТВЕТ  4.5

Answer 2

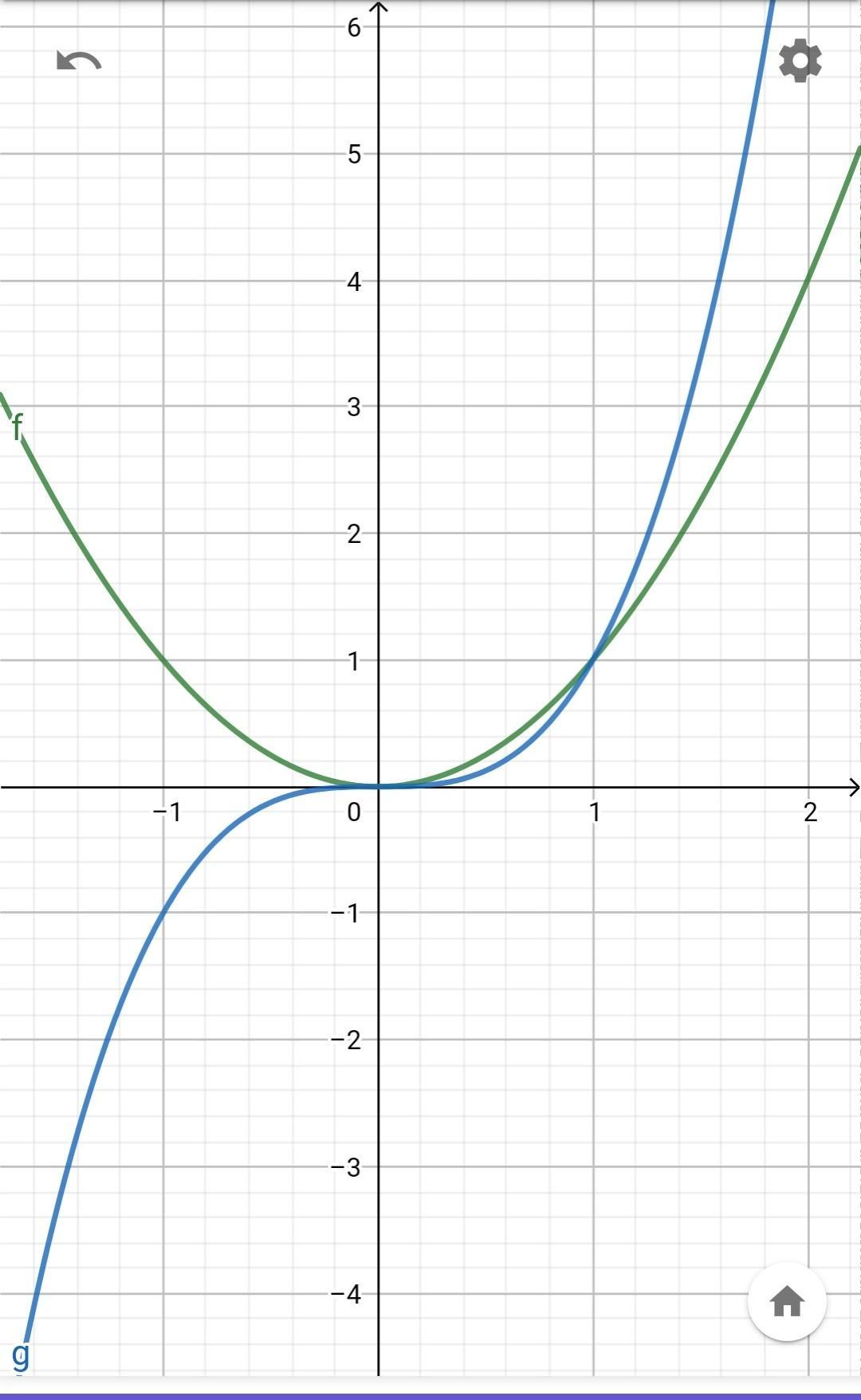
Ответ:

1/12

Пошаговое объяснение:

S = integrate (x^2 - x^3) from 0 to 1

S = x^3/3 - x^4/4 from 0 to 1.

$s = \frac{1}{3} - \frac{1}{4} - (0 - 0)$

$s = \frac{1}{12}$

integrate - знак интеграла