Предмет: Алгебра,
автор: yanameste
Помогите решить!!! Все на фотографии!!!
Приложения:
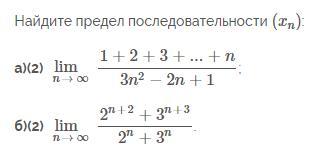
Ответы
Автор ответа:
1
Ответ:
нажимай кнопочки ...
https://znanija.com/task/43644947?utm_source=android&utm_medium=share&utm_campaign=question
Похожие вопросы
Предмет: Українська мова,
автор: tatusya1985
Предмет: Қазақ тiлi,
автор: Kaysarova
Предмет: Русский язык,
автор: nemecpmz
Предмет: Обществознание,
автор: Anonimka89
Предмет: Математика,
автор: Славик122
https://znanija.com/task/43637095