Предмет: Математика,
автор: seregsp
Вычислить неопределенный интеграл
Приложения:
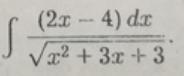
Ответы
Автор ответа:
1
Ответ:
В числителе делаем производную знаменателя:
(x^2+3x+3)' = 2x+3
Приложения:


seregsp:
ошибка картинки, добавь пожалуйста еще раз
не в первый раз уже не показывает ответ программа
загрузила скрины ответа
спасиб)
пожалуйста)
Похожие вопросы
Предмет: Русский язык,
автор: марджина21
Предмет: Английский язык,
автор: Maks1005
Предмет: Русский язык,
автор: Жам25
Предмет: Русский язык,
автор: Настя1221111
Предмет: Математика,
автор: Елиди