Предмет: Математика,
автор: danilasitnikov2001
Нужна помощь в решении)) ( см закрепленное фото)
Приложения:
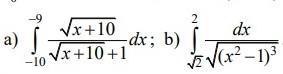
Ответы
Автор ответа:
1
Ответ:
а
б
Похожие вопросы
Предмет: Русский язык,
автор: roma19792
Предмет: Окружающий мир,
автор: Artemisole2015K
Предмет: Английский язык,
автор: sofinavioletta
Предмет: Математика,
автор: Adeliaaaaaasas
Предмет: Математика,
автор: Umnaya7777