Question

СРОЧНО НУЖНО!!!!!!!Геометрия
Прошу решите задачу. Последнюю которая(6)

Answer 1

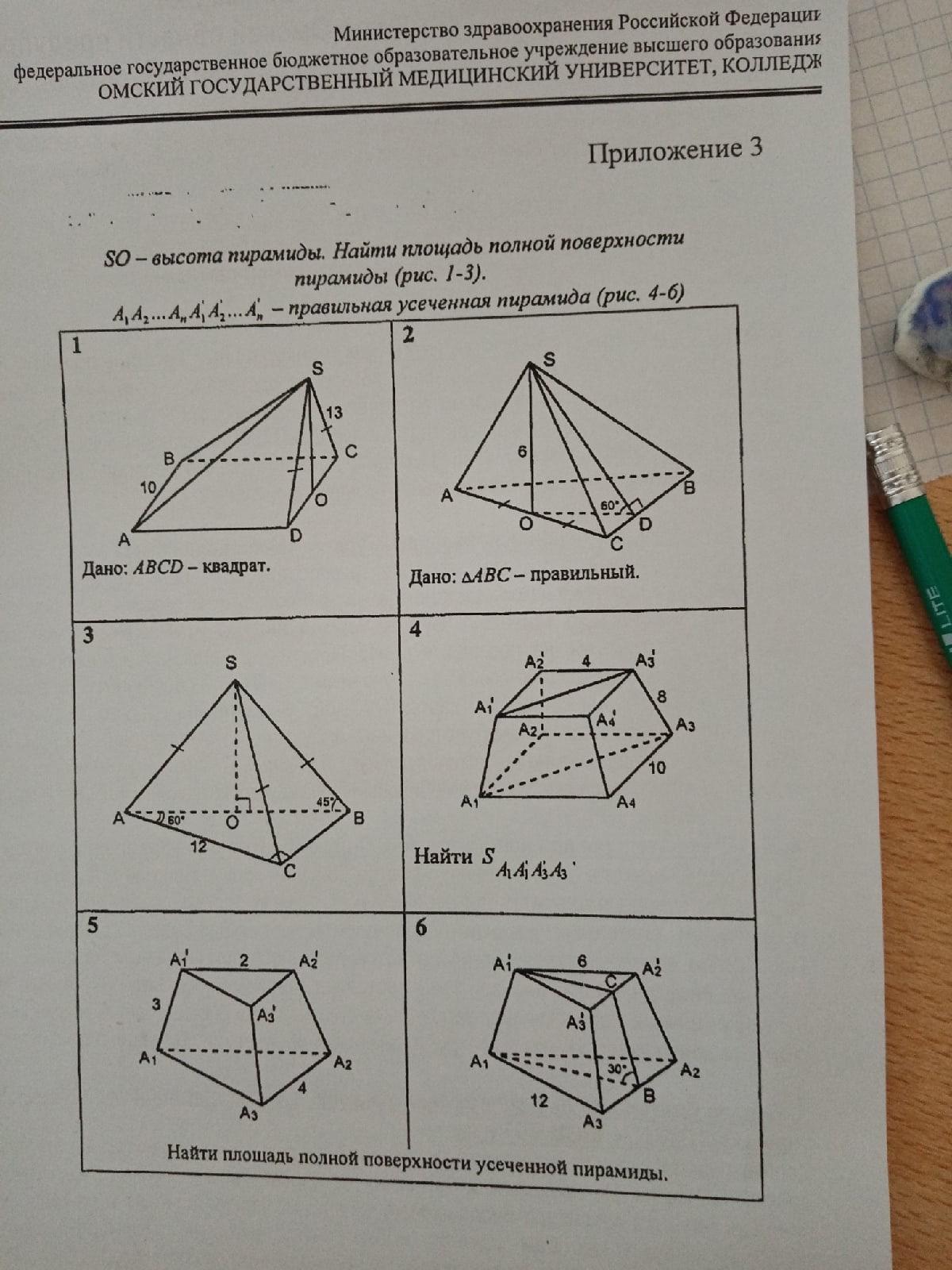
6) Проведём сечение АА1СВ через боковое ребро и апофему.

Фигура в сечении трапеция. Пусть её высота равна h. Основания как высоты в равносторонних треугольниках равны:

А1С = 6*(√3/2) = 3√3.

АВ = 12*(√3/2) = 6√3. Разница между ними равна 3√3.

Из свойств правильной треугольной пирамиды известно, что проекция бокового ребра на основание в 2 раза больше проекции апофемы.

Пусть это будут 2х и х.

Получаем 3х = 3√3, отсюда х = √3.

По условию h/x = tg 30°, тогда h = x*tg 30° = √3*(1/√3) = 1.

Отсюда апофема как гипотенуза при катете против угла 30 градусов равна 2х = 2.

Находим площадь боковой поверхности.

Sбок = 3*((6 + 12)/2)*2 = 3*18 = 48.

Площади оснований S = a²√3/4.

S1 = 6²√3/4 = 9√3.

Sо = 12²√3/4 = 36√3.

Ответ: S = 48+45√3.