Предмет: Алгебра,
автор: nadezhdakhaustova
Помогите Решить тригонометрическое уравнение:
8cos(x)^2+6sin(x)-3=0
Даю 50 баллов
Приложения:
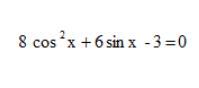
Ответы
Автор ответа:
1
Ответ:
решений нет
Объяснение:
8cos²x+6sinx-3=0
8(1-sin²x)+6sinx-3=0
-8sin²x+6sinx+ 5=0 ,
8sin²x-6sinx- 5=0 , пусть sinx=а , |a|<1
8а²-6а-5=0 , Д=36+160=196 ,
а₁ =(6-14):16=-8\16=-1\2 , sinx=-1\2 , х=-π\6+2πn , x=-5π\6+2πm , n,m∈Z
, а₂=(6+14):16=20\16=5\4=1,25 не подходит под условие |a|<1
nadezhdakhaustova:
Формула корней: -b+- корень из D/ 2a (у нас а = 8)
а₁ =(6-14):(2*8)=-1/2 подходит под условие |a|<1, а₂=(6+14):2=1,25 не подходит под условие |a|<1
а₂=(6+14):(2*8)=1,25 не подходит под условие |a|<1.
Похожие вопросы
Предмет: Русский язык,
автор: ryadnosvetlana
Предмет: Русский язык,
автор: jfsmine911
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: darja120906
Предмет: Алгебра,
автор: Kthf12345Kthf12345