Question

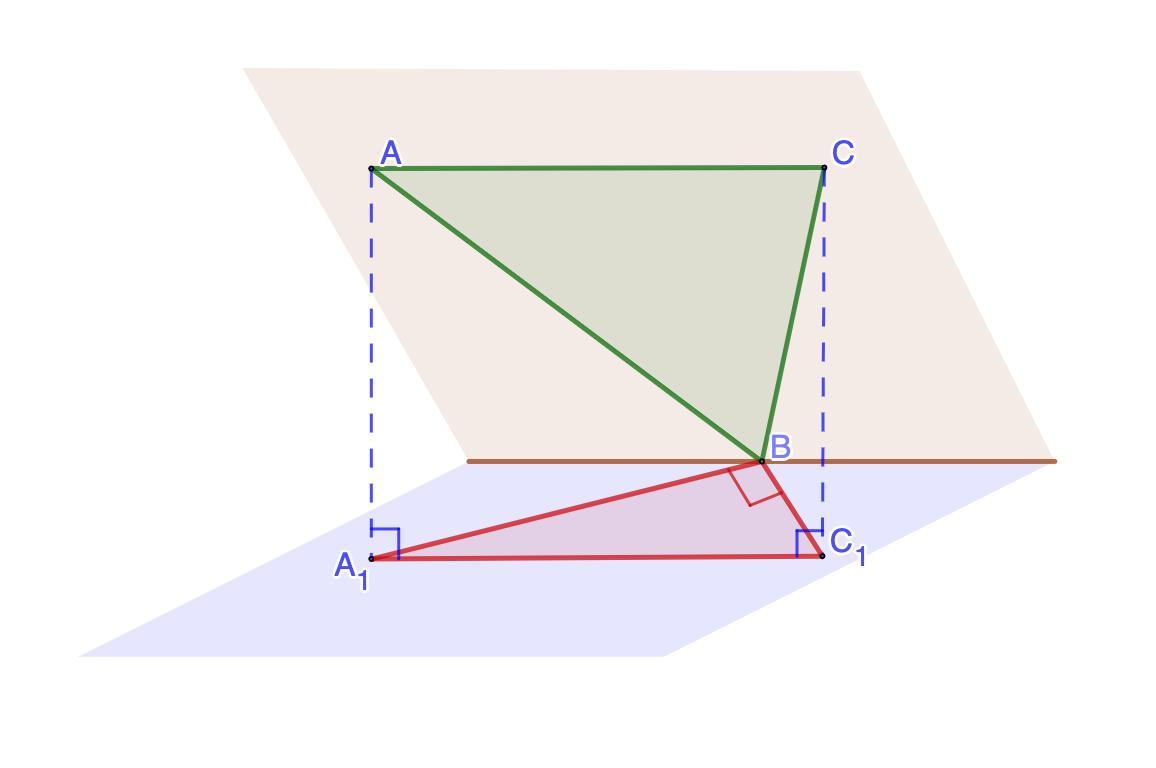
Через вершину В треугольника АВС проведена плоскость, не совпадающая с плоскостью АВС и параллельная его стороне АС. Проекция треугольника АВС на эту плоскость-прямоугольник А1ВС1С прям.углом В. Найдите сторону АС , если ВА1=9см,ВС1=12см(с чертежом!!!)

Answer 1

Ответ:

AC = 15 см

Объяснение:

Дано: $AC \parallel A_{1}BC_{1}$, $\angle A_{1}BC_{1} = 90^{\circ}$, $A_{1}B =$ 9 см, $BC_{1} =$ 12 см

Найти: AC - ?

Решение:

Рассмотрим прямоугольный треугольник Δ$A_{1}BC_{1}$ (так как по условию угол  $\angle A_{1}BC_{1} = 90^{\circ}$).

По теореме Пифагора:$A_{1}C_{1} = \sqrt{A_{1}B^{2} + BC_{1}^{2}} = \sqrt{9^{2} + 12^{2}} = \sqrt{81 + 144} = \sqrt{225} = 15$ см.

Так как по условию треугольник Δ$A_{1}BC_{1}$ - проекция треугольника ΔABC, то прямые $AA_{1}$ и $CC_{1}$ перпендикулярны к прямой $A_{1}C_{1}$, тогда по теореме  $\boxed{AA_{1} \parallel CC_{1}}$.

Так как прямая $A_{1}C_{1}$ - проекция прямой $AC$ на плоскость $A_{1}BC_{1}$ и по условию $AC \parallel A_{1}BC_{1}$, то $\boxed{ AC \parallel A_{1}C_{1}}$.

Четырехугольник $ACC_{1}A_{1}$ - параллелограмм, так как $AA_{1} \parallel CC_{1}$, $AC \parallel A_{1}C_{1}$ по определению. По свойствам параллелограмма его противоположные стороны равны, тогда так как $ACC_{1}A_{1}$ - параллелограмм, то $AC = A_{1}C_{1} = 15$ см.