Предмет: Математика,
автор: hello1401
Вычислите определенный интеграл:
Приложения:
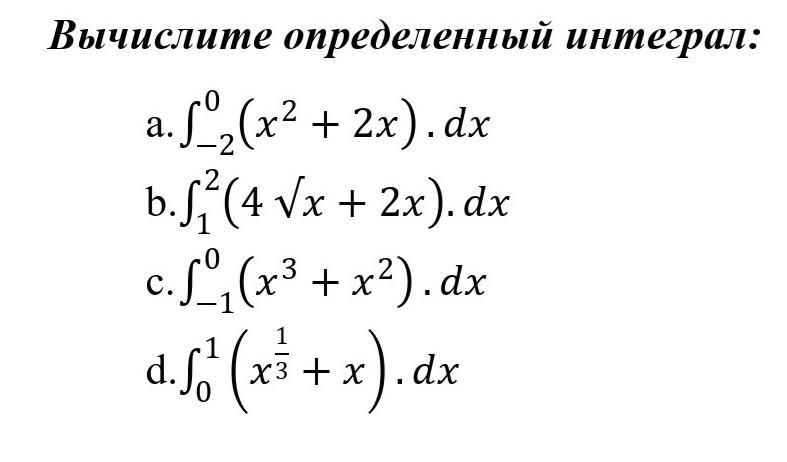
Ответы
Автор ответа:
0
Ответ:
а
б
с
д
Похожие вопросы
Предмет: Русский язык,
автор: XxxMA
Предмет: Русский язык,
автор: Гений95
Предмет: Українська мова,
автор: julia131278
Предмет: Алгебра,
автор: elisawetta2
Предмет: Алгебра,
автор: IgorNikitin97