Предмет: Геометрия,
автор: tvaemin
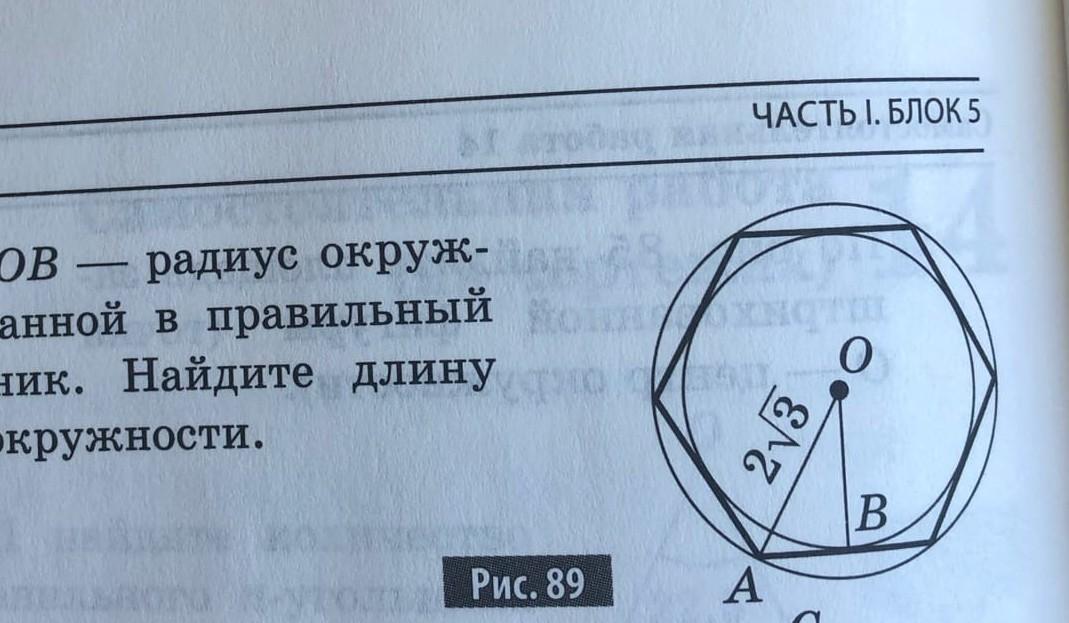
На рис. 89 OB - радиус окружности, вписанной в правильный шестиугольник. Найдите длину вписанной окружности.
Приложения:
Ответы
Автор ответа:
1
Ответ:
OA = стороне правильного шестиугольника!
Объяснение:
АВ = 2√3/2 = √3
ОВ²= (2√3)^2 - (√3)^2 = 9
OB = √9 = 3
C = 2πr
C = 2π·3 = 6π
Похожие вопросы
Предмет: Русский язык,
автор: alabeuw
Предмет: Русский язык,
автор: Elizaveta653
Предмет: Другие предметы,
автор: маки2
Предмет: Математика,
автор: NonA181107
Предмет: Қазақ тiлi,
автор: Лианочка99999