Предмет: Математика,
автор: Arsona
Срочноъ
Помогите......
Приложения:

Ответы
Автор ответа:
0
Ответ:
уравнение касательной и нормали:
Пошаговое объяснение:
Дано:
1) Найдем значение у в точке:
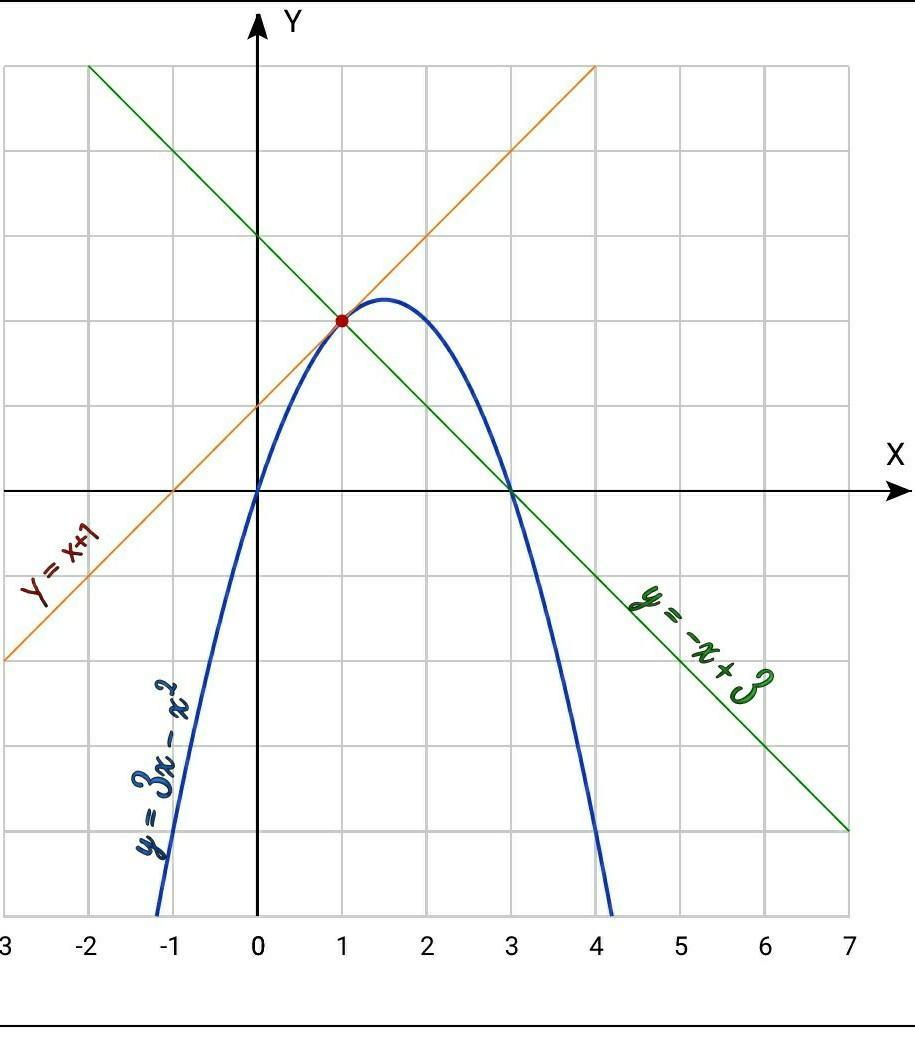
Ищем касательную и нормаль к графику ф-ии
в точке (1; 2)
2) Найдем производную у':
3) Найдем значение производной в точке касания:
у'(х0) - это угловой коэффициент касательной k, или tg угла касательной с осью Ох. В нашем случае k = 1
4) Находим формулы:
а) уравн. касательной:
Подставим известные значения:
б) уравн. нормали:
Подставляем известное:
Итак:
уравнение касательной и нормали:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: сальникова20022015
Предмет: Русский язык,
автор: Rushida20051
Предмет: Математика,
автор: vasek1978
Предмет: География,
автор: дима200523