Question

Найдите медиану, проведённую к гипотенузе, если один из катетов равен 6см, а площадь треугольника 24см2

Answer 1

Ответ:

Дано:

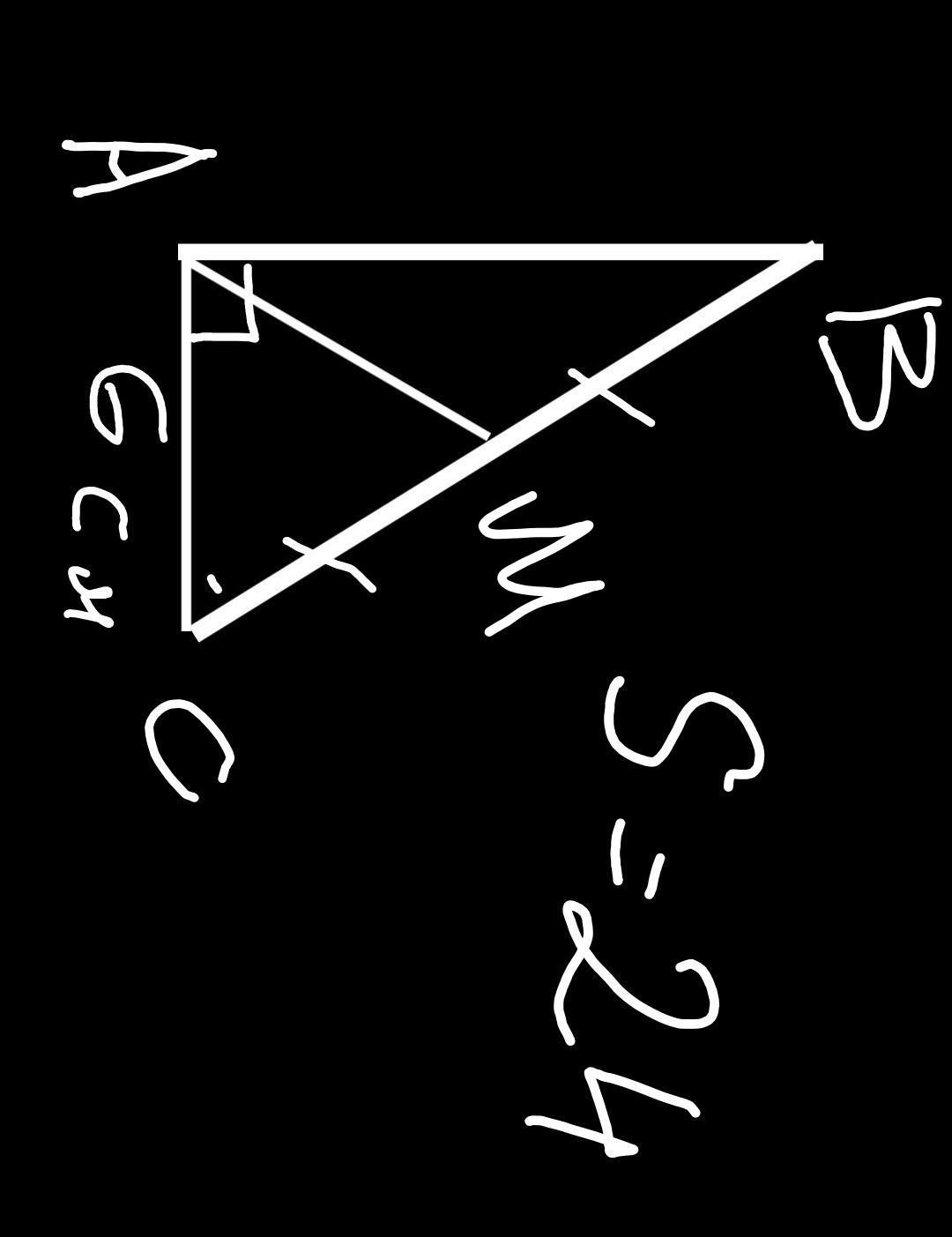
треугольник АВС- прямоугольный

АМ- медиана

АС=6 см

S ABC=24см²

Найти:

АМ-?см

Решение.

S ABC= ½ AB×AC=½×6×АВ=3АВ=24 см²

АВ=24:3=8см

По т. Пифагора (треугольник АВС- прямоугольный): ВС²=АВ²+АС²

ВС²=8²+6²

ВС²=64+36

ВС²=100

ВС=

$+ - \sqrt{100}$

(ВС не равно

$- \sqrt{100}$

, т.к. длина- положительная величина)

ВС=10 см

В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.

АМ=ВС:2=10:2=5 cм

Ответ: АМ=5см.