Предмет: Геометрия,
автор: prossasa6
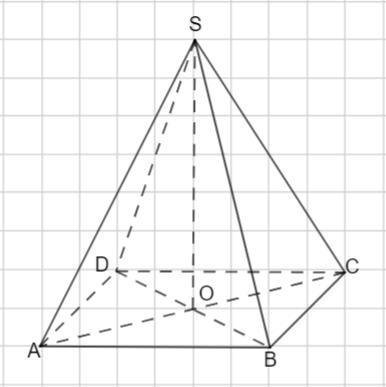
Дана правильная четырехугольная пирамида SABCD. Найдите бокове ребро пирамиды, если AB=8, а SO=7.
Ответы
Автор ответа:
0
Ответ:
9 ед.
Объяснение:
Пусть задана SABCD - правильная пирамида.
ABCD - квадрат, АВ= 8 ед.
Высота пирамиды SО= 7 ед.
Диагональ квадрата равна , где а -сторона квадрата. Значит,
ед.
Диагонали квадрата пересекаются точкой пересечения пополам.
ед.
Рассмотрим треугольник АSО - прямоугольный.
По теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Значит, боковое ребро пирамиды равно 9 ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: tatusj168
Предмет: Английский язык,
автор: БАНАНЧИК3000
Предмет: Русский язык,
автор: mariam1222
Предмет: Информатика,
автор: maksrubinov
Предмет: Русский язык,
автор: dhduhfje