Предмет: Геометрия,
автор: LonelyPussycat
взываю на помощь (с рисунком пожалуйста)
Приложения:

siestarjoki:
DE/BC =2/3
медианы делятся 2:1 от вершины
Ответы
Автор ответа:
2
Медианы треугольника пересекаются в одной точке и делятся ей в отношении 2:1 от вершины.
Пусть AN - медиана, AM/MN =2/1
△DAE~△BAC (стороны параллельны)
AM, AN - соответствующие отрезки в подобных треугольниках, их отношение равно коэффициенту подобия.
(BDEC - трапеция, пересечение боковых сторон и середины оснований лежат на одной прямой. M - середина DE)
DE/BC =AM/AN =2/3 => BC =6*3/2 =9
Приложения:
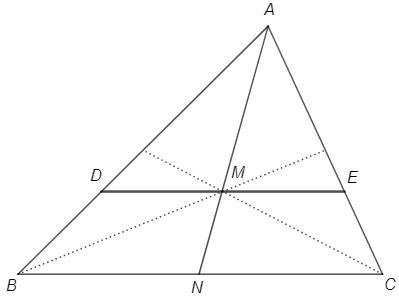
необязательно доказывать, что M - середина. Достаточно, что луч AN в обоих треугольниках отложен на равный угол от соответствующих сторон.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: mazda5949
Предмет: Английский язык,
автор: ученица152
Предмет: Математика,
автор: liza1578
Предмет: Русский язык,
автор: tarn2005