Предмет: Математика,
автор: addax0
Задачи на производные
Помогите кто чем может
Приложения:

pushpull:
всё это решаемо и не сложно, но впихнуть в один ответ просто нереально. поделите на части....
На части боюсь монет не хватит...
тогда ждите. попытаюсь сюда втиснуть
У меня не хватит слов чтобы выразить Вам свою благодарность! И тем не менее, спасибо огромное!!
не за что. обращайтесь, чес смогу, помогу -))
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1. производные
(5x³-3x⁹)' = 5*3x² -3*9x⁸ = 15x² -27x⁸
(e⁻⁵ˣ)' = -5e⁻⁵ˣ
2.
3. уравнение касательной
f'(x) = -2x+6
f(x₀) = f(-2) = -8
f'(x₀) = f'(-2) = 10
или
5.
для всего ниже потребуется производная
f'(x) = (x³-2x²+x+3)' = 3x² -4x +1
а) стационарные точки
3x² -4x +1 = 0 ⇒ x₁ = 1; x₂ = 1/3
б) экстремумы
f(1) = 3 - минимум
f(1/3) = 85/27 максимум
в) возрастание и убывание
по стационарным точкам получили три интервала
смотрим на каждом значение производной и определяем возрастание или убывание функции
(-∞ ;1/3) f'(0) =1 > 0 функция возрастает
(1/3; 1) f'(2/3) = -1/3 < 0 функция убывает
(1; +∞) f'(10) = 261 > 0 функция возрастает
г) график прилагается (таблицу уже сами построите)
Приложения:
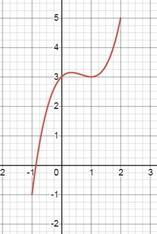
фуф... втиснула
Человек с большой буквы иначе не скажешь...
-)))
рада, что смога помочь
Похожие вопросы
Предмет: Окружающий мир,
автор: innafokina74
Предмет: Русский язык,
автор: tabenkina
Предмет: Русский язык,
автор: LizaKorschakova
Предмет: Математика,
автор: ilinafredlin1
Предмет: Английский язык,
автор: Мария20052018