Предмет: Математика,
автор: Serafimka92
Найти производные заданных функций
Приложения:
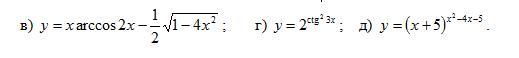
Ответы
Автор ответа:
2
Ответ:
в
г
д
Serafimka92:
Спасибон, а можешь пож ссылку на прогу кинуть?
это на brainly. Встроенная. Я ввожу символы сама, и они выводятся в красивой форме
но решение мое
то есть это не калькулятор
А понял, спасибо большое
А можно ваш вк? :) :) :)
в лс
Похожие вопросы
Предмет: Русский язык,
автор: Ярешутебя
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ella7848
Предмет: Математика,
автор: larashiman
Предмет: Физика,
автор: Veronika01001