Предмет: Математика,
автор: valentinastepanovna
7 задание помогите пожалуйста
Приложения:
Ответы
Автор ответа:
1
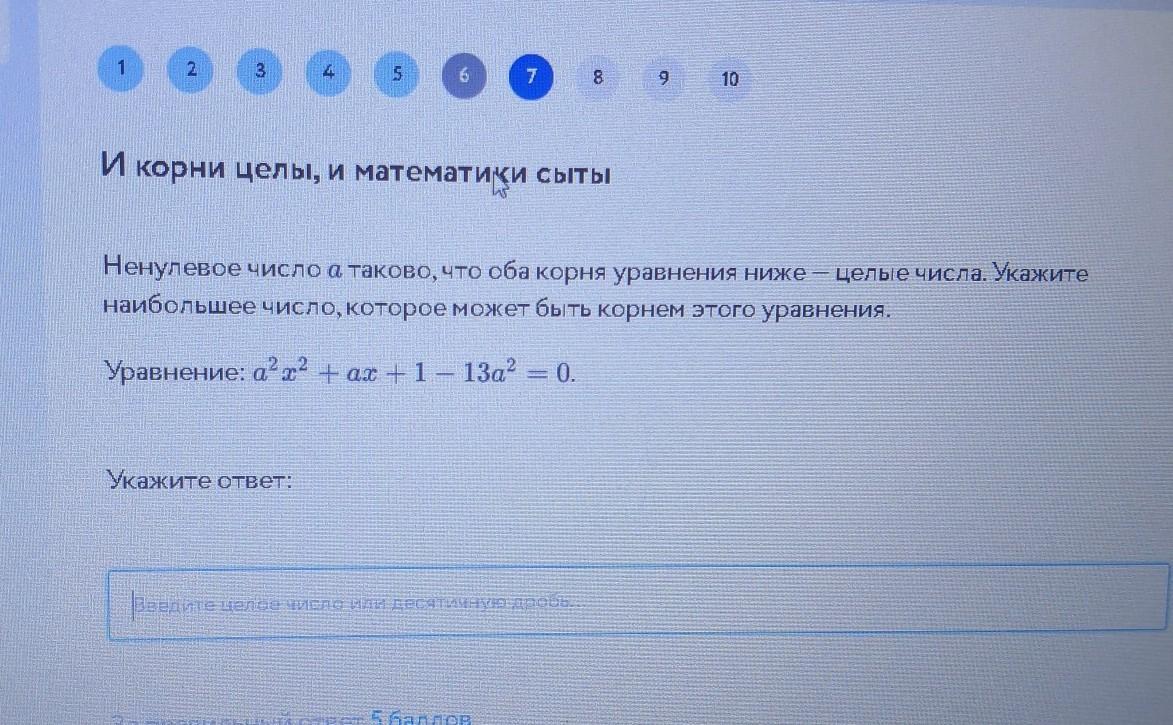
Имеем квадратное уравнение:
a²x² + ax + 1 - 13a² = 0
Т.к., по условию, а ≠ 0, разделим обе части уравнения на а²:
x² + x/a + 1/a² - 13 = 0
по т. Виета:
x1 + x2 = -b = -1/a (1)
x1 • x2 = c = 1/a² - 13 (2)
Т.к., по условию задачи, x1 и х2 - целые числа, то: (х1 + х2) и (х1 • х2) - тоже целые числа.
Тогда, для удовлетворения вышеуказанного в (1) и (2) подходит лишь а = ±1.
Имеем:
х1 + х2 = -1/а = -1/±1 = ±1
х1 • х2 = 1/а² - 13 = 1/(±1)² - 13 = -12
Откуда:
х1 = -4; х2 = 3 (при а = 1)
или
х1 = -3; х2 = 4 (при а = -1)
Наибольший корень х = 4 (при а = -1)
Похожие вопросы
Предмет: Русский язык,
автор: baiwa
Предмет: Русский язык,
автор: Angellina3933
Предмет: Русский язык,
автор: fidhus616
Предмет: Другие предметы,
автор: maks8888881