Question

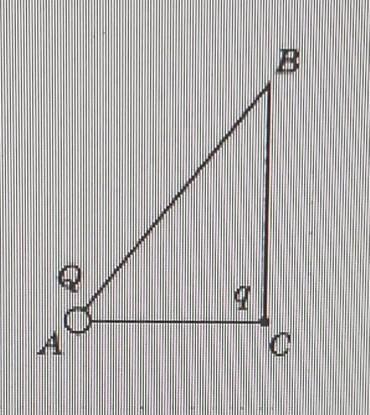
В ввершине А прямоугольного треугольника АВС находит-
ся точечный заряд Q(см. рисунок). Он действует с силой
25 мкн на точечный заряд а, помещённый в вершину с.
Определите, с какой силой будут взаимодействовать за-
ряды, если заряд перенести в вершину B. Отношение сторон AC/AB=0.6​

Answer 1

Ответ:

$F_{Q_{B}} \approx 14,06$ мкH

Примечание:

По условию задачи заряд Q из точки А переместили в точку B

Объяснение:

Дано:

Q

q

$F_{Q_{A}} = 25 \cdot 10^{-6} \ \rm H$

$\dfrac{AC}{AB} = 0,6$

Найти:

$F_{Q_{B}} - \ ?$

---------------------------

Решение:

По закону Кулона:

$F_{k} = \dfrac{k \cdot q_{1} \cdot q_{2}}{r^{2}}$

$F_{Q_{A}} = \dfrac{k \cdot Q \cdot q}{r_{1}^{2}} = \dfrac{k \cdot Q \cdot q}{AC^{2}}$

$F_{Q_{B}} = \dfrac{k \cdot Q \cdot q}{r_{2}^{2}} = \dfrac{k \cdot Q \cdot q}{BC^{2}}$

По условию задачи и теореме Пифагора:

$\displaystyle \left \{ {{AB^{2} = AC^{2} + CB^{2} } \atop { \dfrac{AC}{AB} = 0,6 }} \right$    $\displaystyle \left \{ {{AB^{2} = AC^{2} + CB^{2} } \atop { AC = 0,6AB }} \right$   $\displaystyle \left \{ {{AB^{2} = AC^{2} + CB^{2} } \atop { AC^{2} = (0,6AB)^{2} }} \right$

$\displaystyle \left \{ {{AB^{2} = AC^{2} + CB^{2} } \atop { AC^{2} = 0,36AB^{2} }} \right \Longrightarrow AB^{2} = 0,36AB^{2} + CB^{2}$

$AB^{2} = 0,36AB^{2} + CB^{2}$

$BC^{2} = 0,64AB^{2}$

$\dfrac{F_{Q_{B}}}{F_{Q_{A}}} = \dfrac{\dfrac{k \cdot Q \cdot q}{BC^{2}}}{\dfrac{k \cdot Q \cdot q}{AC^{2}}} = \dfrac{k \cdot Q \cdot q \cdot AC^{2}}{k \cdot Q \cdot q \cdot BC^{2}} = \dfrac{AC^{2}}{BC^{2}} = \dfrac{0,36AB^{2}}{0,64AB^{2}} = 0,5625;$

$\dfrac{F_{Q_{B}}}{F_{Q_{A}}} = 0,75 \Longrightarrow F_{Q_{B}} = 0,5625 F_{Q_{A}}$

$F_{Q_{B}} = 0,5625 \cdot 25 \cdot 10^{-6} \ \rm H = 14,0625 \cdot 10^{-6} \ \rm H \approx 14,06 \cdot 10^{-6}$

Ответ: $F_{Q_{B}} \approx 14,06$ мкH.