Предмет: Алгебра,
автор: Аноним
Знатоки помогите пожалуйста с тремя задачами по алгебре! пожалуйста!
Приложения:
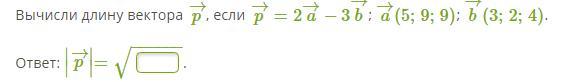


Ответы
Автор ответа:
1
Найдём координаты вектора . Для этого все координаты вектора
нужно умножить на 2:
По такому же принципу найдём координаты вектора :
Чтобы найти координаты вектора , вычтем соответствующие координаты:
Длина произвольного вектора вычисляется по формуле
:
Ответ: .
***
Координаты середины отрезка есть среднее арифметическое координат конца отрезка:
***
По условию точка делит сторону
пополам (и так же с двумя другими точками). Найдём координаты точки
Расстояние между точками и
(т. е. длина медианы) равно:
То есть .
То же самое проделаем с двумя другими медианами:
- - - - - - -
***
Если что-либо будет непонятно — спрашивайте.
mvolturi:
https://znanija.com/task/43603688 Добрый день! Извините что отвлекаю, но можете посмотреть и мое задание? Пожалуйста, не понимаю как решать
Похожие вопросы
Предмет: Русский язык,
автор: ksyusham04
Предмет: Окружающий мир,
автор: antonovand
Предмет: Русский язык,
автор: anver2007
Предмет: Математика,
автор: alenas655