Предмет: Математика,
автор: starova82
Найдите неопределённый интеграл
Приложения:
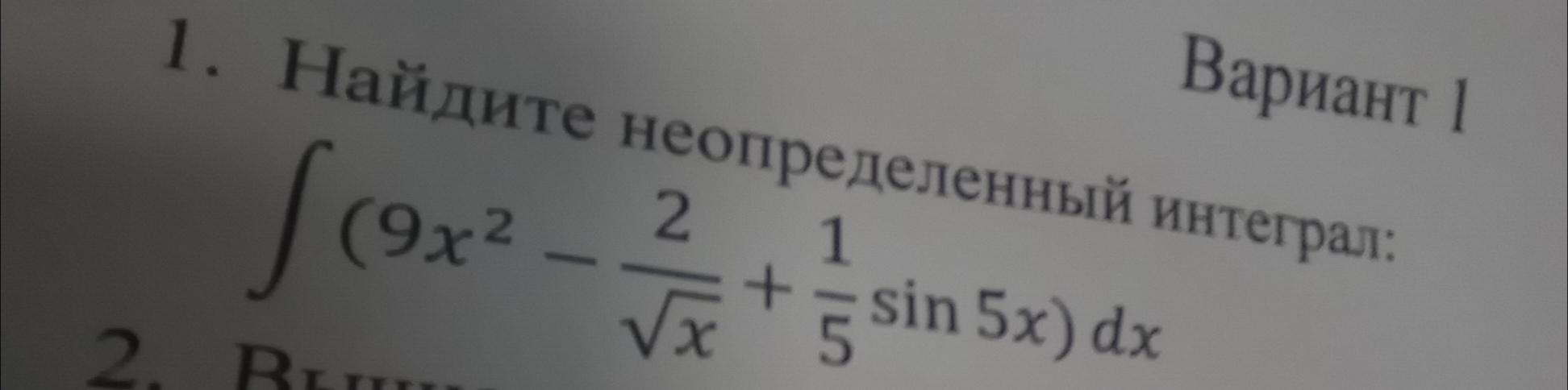
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: dfikdfik
Предмет: Русский язык,
автор: оле6
Предмет: Русский язык,
автор: айрисхамзина
Предмет: Математика,
автор: ElzhanAbish
Предмет: Қазақ тiлi,
автор: моти5