Дана правильная треугольная призма ABCA1B1C1, в которой сторона основания AB = 8, боковое ребро AA_1= 2 корень из 2 . Точка Q — точка пересечения диагоналей грани ABB1А1, точки M, N и K — середины ВС, СC1 и А1C1 cответственно.
а) Докажите, что точки Q, M, N и K лежат в одной плоскости.
б) Найдите площадь сечения QMN.
Без метода координат
Ответы
Ответ:
а) Доказательство в объяснении.
б) Площадь сечения равна 18√2 ед².
Пошаговое объяснение:
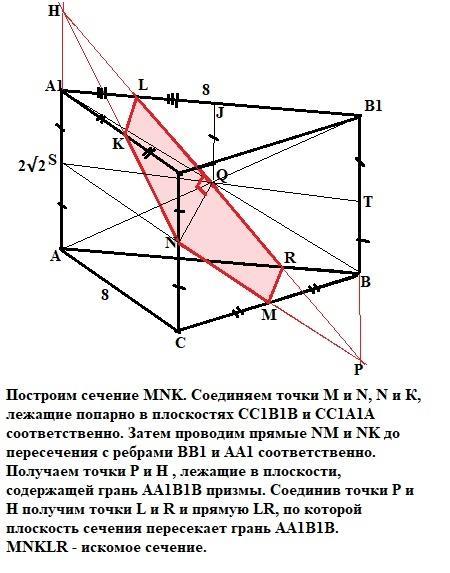
Для начала построим сечение MNK. Соединяем точки M и N, N и К, лежащие попарно в плоскостях СС1В1В и СС1А1А соответственно. Затем проводим прямые NM и NK до пересечения с ребрами ВВ1 и АА1 соответственно. Получаем точки Р и Н , лежащие в плоскости, содержащей грань АА1В1В призмы. Соединив точки Р и Н получим точки L и R и прямую LR, по которой плоскость сечения пересекает грань АА1В1В. MNKLR - искомое сечение.
а) Теперь надо доказать, что прямая LR проходит через точку Q.
Точка пересечения диагоналей - центр прямоугольника АА1В1В, следовательно, прямая ST, проходящая через середины сторон АА1 и ВВ1, параллельная АВ и А1В1, проходит через точку Q.
Тогда в равных по двум катетам (SH = ТР и SQ = TQ) прямоугольных треугольниках SHQ и TPQ отрезки A1L и BR равны, как соответственные средние линии. Треугольники QA1L и BRQ равны по двум сторонам (QA1=QR - A1B диагональ прямоугольника А1L = BR) и углу между ними (∠LA1Q = ∠RBQ, как накрест лежащие углы при параллельных АВ и А1В1 и секущей А1В).В равных углах против равных сторон лежат равные углы. Значит ∠А1QL = BQR. А так как А1В - прямая, то ∠А1QL и BQR - вертикальные и по определению LR - прямая, проходящая через точку Q. Следовательно, сечение проходит через точку Q и точки Q, M, N и K лежат в плоскости сечения, что и требовалось доказать.
б) Отметим, что ∠LQN = RQN = 90° так как QN параллельна плоскости основания, а плоскость АА1В1В перпендикулярна плоскости основания. KL║NQ║MR.
Тогда QNKL и QNMR - равные прямоугольные трапеции.
В трапеции NKLQ основания NQ = (√3/2)·a (как высота правильного треугольника) NQ = (√3/2)·8 = 4√3 ед.
KL = (1/2)·NQ = 2√3 ед. (средняя линия треугольника NHQ).
LQ = √(LJ²+JQ²) = √(4+2) = √6 ед. (по Пифагору).
Площадь трапеции Snklq = (KL+NQ)·LQ/2 = (2√3+4√3)·√6/2 = 9√2 ед².
Тогда Snklrm = 2·Snklq = 18√2 ед².