Question

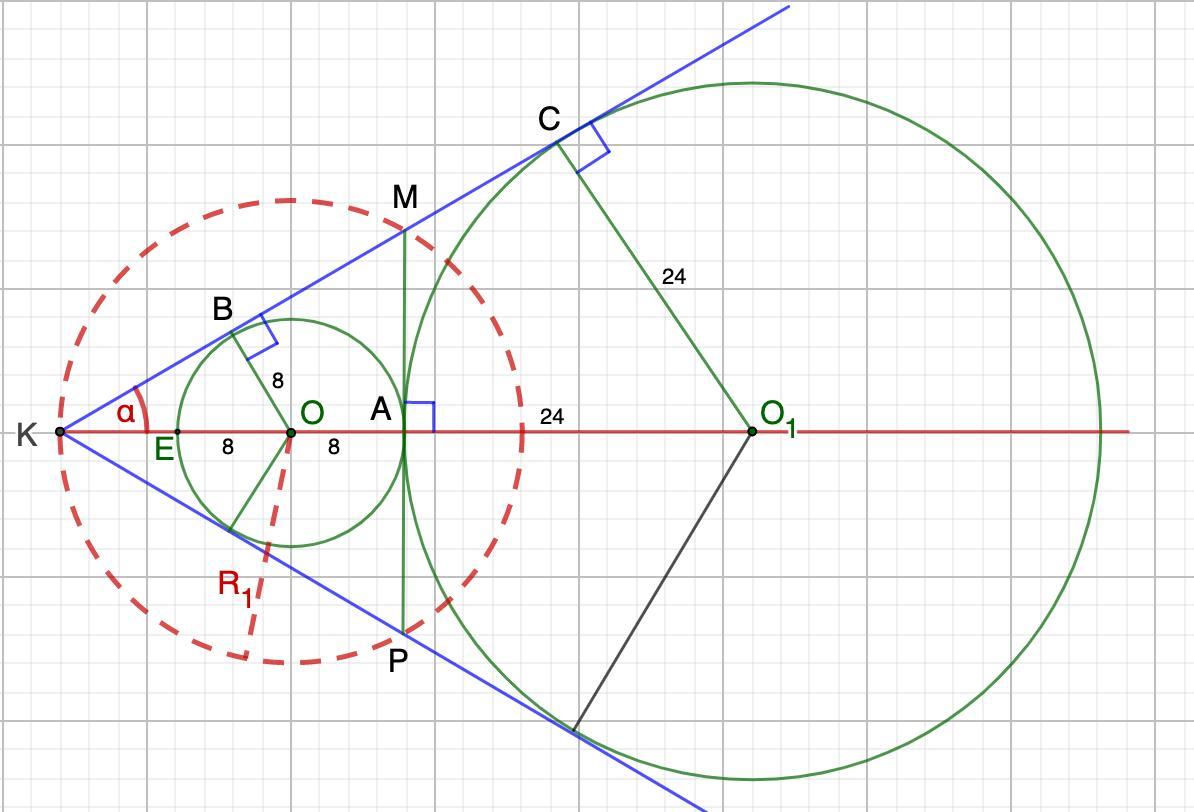
две касающиеся внешним образом в точке А окружности радиусы, которых равны 8 и 24, в
вписаны в угол с вершиной К. Общая касательная к этим окружностям, проходящая через точку А, пересекает стороны угла в точке М и Р. Найдите радиус окружности, описанной около треугольника МРК. ​Пожалуйста помогите!!!​

Answer 1

Ответ:

$\boxed{R_{\bigtriangleup MPK} = 16}$

Объяснение:

Дано: OC = 8, BA = 24, MP - касательная к окружностям; O,B - центры окружностей

Найти: $R_{\bigtriangleup MPK}$ - ?

Решение:

Центры окружностей, вписанных в угол, лежат на биссектрисе угла, КВ – биссектриса угла К.

Проведем OF и ВТ – радиусы в точки касания окружностей со стороной угла.

OF⊥KT, BT⊥KT по свойству касательной.

Треугольник ΔKOF подобен треугольнику ΔKBT по двум углам (так как угол ∠TKB - общий, а ∠OFK = ∠BTK = 90°), следовательно

$\frac{BT}{FO} = \frac{BK}{OK} \Longrightarrow BT * OK = FO * BK$.

BT * OK = FO * BK

BA * OK = OC * BK

AB * (OC + KC) = OC * (CO + OA + AB + KC)  

AB * (OC + KC) = OC * (2CO + AB + KC)

24(8 + KC) = 8(2 * 8 + 24 + KC)

192 + 24KC = 8(40 + KC)|:8

24 + 3KC = 40 + KC

2KC = 16

KC = 8

KO = KC + CO = 8 + 8 = 16

В прямоугольном треугольнике KFO катет OF = 8,  гипотенуза KO = 16, значит угол FKO равен 30 градусам.

Тогда угол МКР равен 60 градусам (КВ - биссектриса)

ОА и ВА – радиусы, проведенные в точку касания, значит ОВ⊥МР по свойству касательной.

КА – высота и биссектриса треугольника МКР, значит он равнобедренный, а так как угол К равен 60 градусов, то треугольник равносторонний.

Радиус окружности, описанной около равностороннего треугольника равен 2/3 его высоты:

КА = КС + АС = 8 + 16 = 24

R = 2/3 KA = 2/3 * 24 = 16

Answer 2

Ответ:

16 см.

Объяснение:

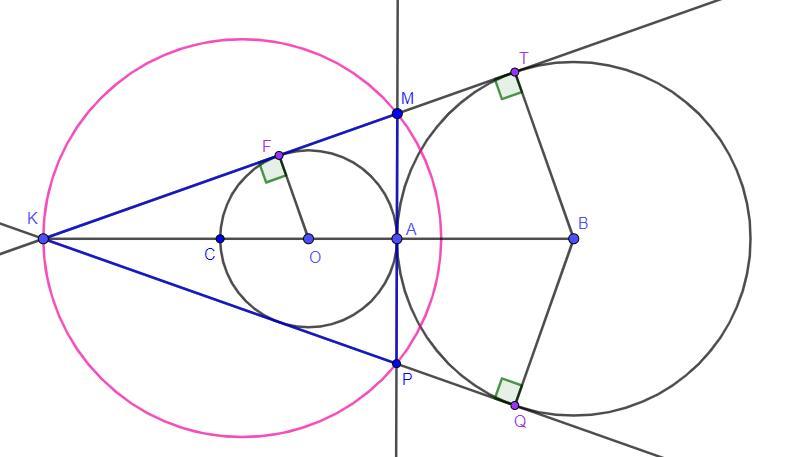
Дано: Окр.Оr и Окр.О₁R касаются внешним образом в точке А.

r=8 см; R=24 см.

КМ, КР - касательные.

МР - общая касательная

Найти: R₁ - радиус описанной окружности около ΔКМР.

Решение:

1. Рассмотрим ΔКВО и ΔКСО₁ - прямоугольные (радиус ⊥ касательной)

α - общий.

⇒ ΔКВО ~ ΔКСО₁

Составим пропорцию:

$\frac{OB}{O_1C}=\frac{KE+EO}{KT+EO_1}\\\frac{8}{24}=\frac{KE+8}{KE+40}\\8KE+320=24KE+192\\KE=8(cm)$

2. Рассмотрим ΔКВО - прямоугольный.

КО=КЕ+ЕО=8+8=16 (см); ВО=8 см

⇒α=30° (катет равен половине гипотенузы)

3. Рассмотрим ΔКМА - прямоугольный (общая касательная ⊥ прямой, соединяющей центры)

Пусть АМ=х, тогда КМ=2х (катет, лежащий против угла 30°)

По теореме Пифагора:

КМ²=АМ²+КА²

4х²=х²+24²

х²=192

х=8√3

⇒ АМ=8√3 см, тогда КМ=16√3 см.

4. Рассмотрим ΔРКМ.

АК - высота, биссектриса (центр вписанной окружности лежит на биссектрисе)

⇒ΔРКМ - равнобедренный.

⇒∠КРМ=∠КМР (при основании р/б Δ)

∠К=60° (КА-биссектриса) ⇒∠КРМ=∠КМР=60° (сумма углов Δ)

ΔРКМ - равносторонний.

5. Радиус описанной окружности около равностороннего треугольника:

$R=\frac{a}{\sqrt{3} }$

Тогда:

$R_1=\frac{KM}{\sqrt{3} } =\frac{16\sqrt{3} }{\sqrt{3} } =16(cm)$