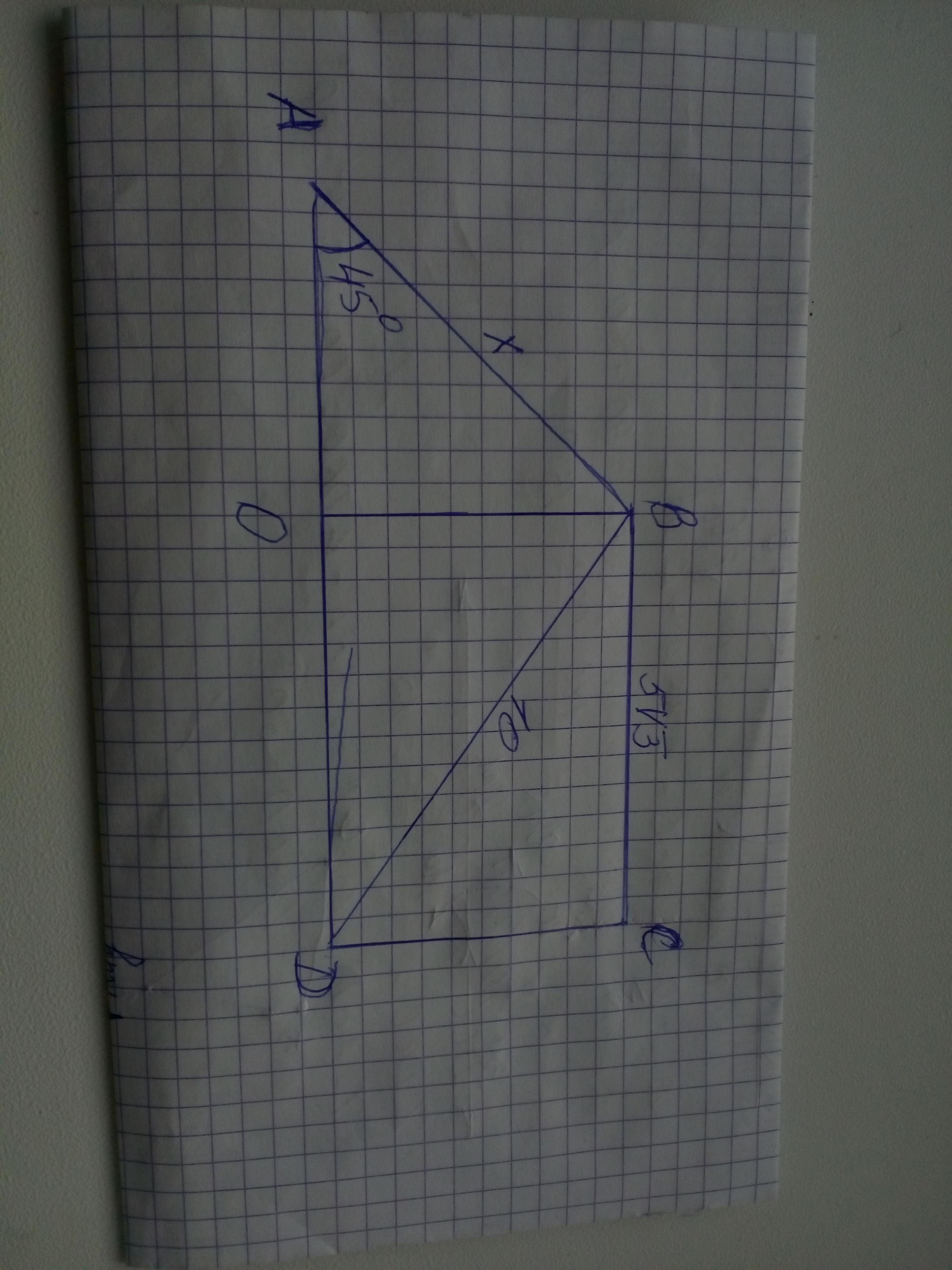
в прямоугольной трапеции ABCD с основаниями AD и bc диагональ bd равна 10 , а угол A равен 45 грдаусам . найдите бОльшую боковую сторону , если меньше основание трапеции равно 5√3
Ответы
Ответ:5√2
Пошаговое объяснение: при проведении диагонали ВD образуется прямоугольный треугольник ВСD. По теореме Пифагора находим высоту трапеции СD=√(ВD²-ВС²)=√(10²-(5√3)²√(100-75)=√25=5 см. Угол А =45° и если провести высоту с вершины В, то образуется равнобедренный прямоугольный треугольник АОВ, у которого длина высоты ВО будет равна длине второго катета АО=5. Так как равнобедренный прямоугольный треугольник одновременно является равнобедренный и прямоугольным при условии, что его острые углы равны 45°. Один угол задан по условию 45°, а второй находим из условия, что сумма острых углов в прямоугольном треугольнике равна 90°. Значит второй угол будет равен: 90-45=45°. Поэтому длина большей боковой стороны равна: АВ=√(ВО²+АО²)=√(5²+5²)=√50=5√2