Предмет: Математика,
автор: alina564295
Найдите производные следующих функций и Найдите производные следующих начения функций в точке х=1
Приложения:
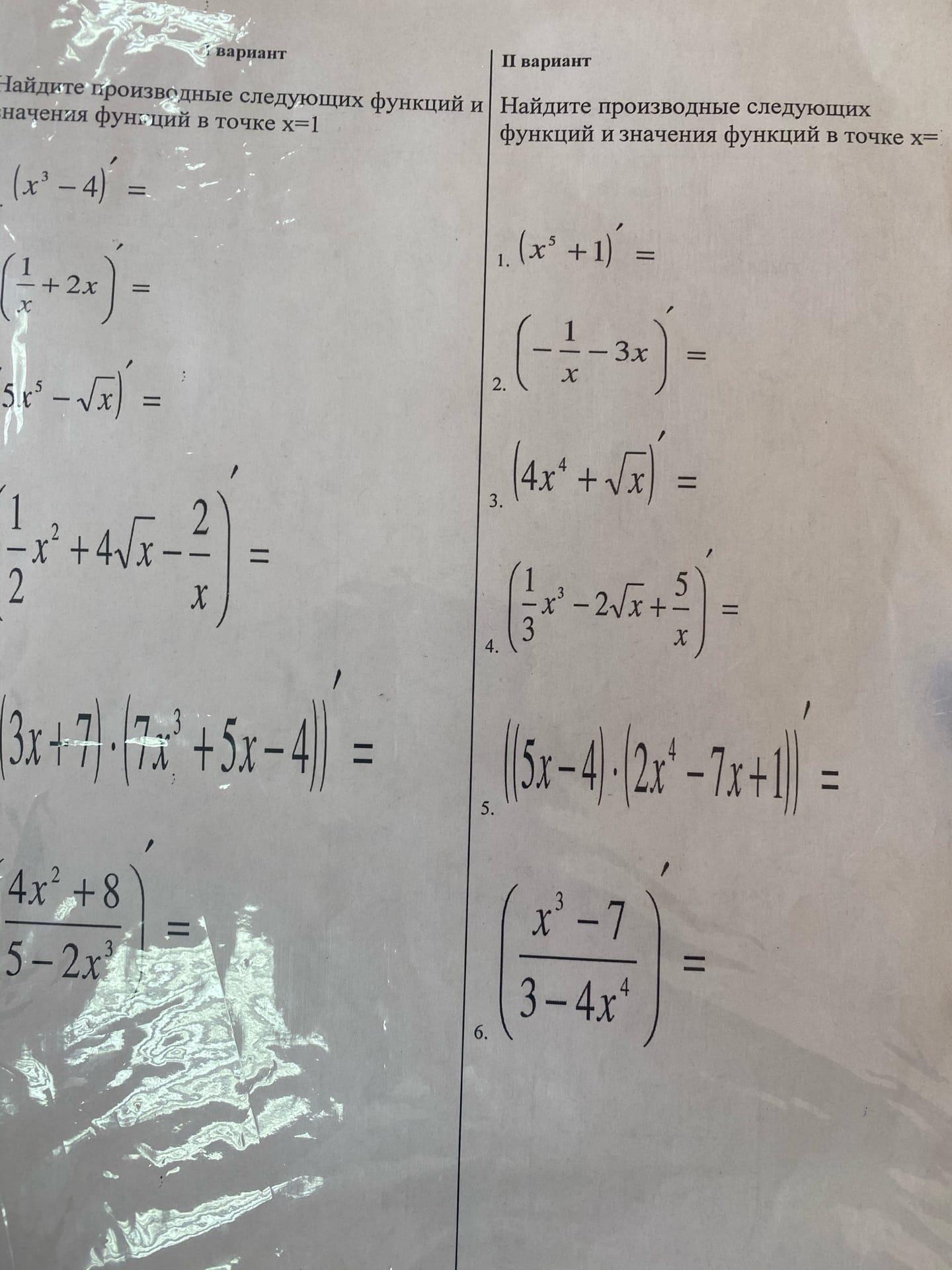
Ответы
Автор ответа:
1
Ответ:
1
2
3
4
5
6
alina564295:
Спасибо большое ЛУЧШАЯ ♥️
Похожие вопросы
Предмет: Русский язык,
автор: масуша1
Предмет: Окружающий мир,
автор: динара0710
Предмет: Другие предметы,
автор: Ангелисия
Предмет: Математика,
автор: leraokssis
Предмет: Окружающий мир,
автор: elieli89