Question

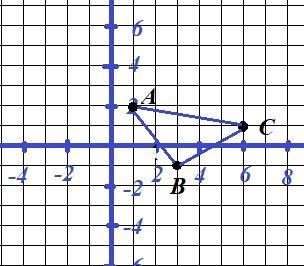
Докажите, что треугольник с вершинами A(1; 2), B(3; −1), C(6; 1) является прямоугольным и равнобедренным.

рисунок обязательно, прошу!!!!!!!!!!!!

Answer 1

Ответ:

Объяснение:

Докажите, что треугольник с вершинами A(1; 2), B(3; −1), C(6; 1) является прямоугольным и равнобедренным.

Длина стороны АВ равна

AB²=(x2-x1)² + (y2-y1)² = (3-1)² + (-1-2)² = 2²+(-3)² = 4+9=13;

AB=√13;

------------------

BC²=(6-3)² + (1 -(-1))²= 3² + 2² = 9+4=13;

BC=√13;

AB=BC - треугольник равнобедренный.

Найдем АС:

АС² = (6-1)² + (1-2)² = 5²+(-1)²=25+1=26;

AC=√26;

------------

Если треугольник прямоугольный, то выполняется теорема Пифагора:

AC²=AB²+BC²;

(√26)²=(√13)²+(√13)²;

26 = 13 + 13;

26=26, что и требовалось доказать.

Треугольник АВС - прямоугольный и равнобедренный